1998-11-20[n年前へ]
■モアレはデバイスに依存するか? 
まず、以下のような2つの同心円画像をつくる。(なお、このような画像を簡単に作るために、Photoshop用のフィルターを作った。詳しくは「Photoshopの同心円フィルターを作る。」を参照して頂きたい。)以下の2つの画像は少し中心位置がずれている。また白く見えるところは255の値を持ち、黒く見えるところは0の値を持っている。(画像自体は512x512であり、表示の際に128x128に変換している。だから、この画像をそのまま保存して頂ければ、512x512のサイズで保存することができる。)
 |
 |
- 黒(0)+黒(0)=0(すなわち黒)
- 白(255)+白(255)=255(すなわち白)
- 黒(0)+白(255)=255(すなわち白)
- 画像1を白黒反転し、画像1'を作る。
- 画像2を白黒反転、画像2'を作る。
- 画像1'と画像2'を加算し、画像3を作成する。
- 画像3を白黒反転し、画像3'を作成する。
 |
それでは、以上の画像変換を小さい画像でまとめて表示してみる。
 |  |  |
ところで、上の3つの画像をそれぞれ平滑化してみる。すると、以下のようになる。
 |  |  |
以下でもう少し詳しく考えてみる。
重ね合わせにおける加算演算
下のような画像A、画像Bを考える。拡大してあるが、画像自体は1x2ピクセルのサイズである。また、白=255、黒=0とすれば、いずれも平均値は128程度である。 |  |
- 黒+黒=黒
- 白+白=白
- 黒+白=黒
 |  |  |
 |  |  |
 |  |  |
これに平均値も示すと以下のようになる。ここでは、LBPなどの紙に出力する際によく使われる、白=0、黒=255という表記をする。
 |  |  |
 |  |  |
 |  |  |
同じ128+128でも、結果は128になるか256になるかの2種類ある。同じもの同士であれば、結果は128であるし、そうでなければ256になる。そのために、平均値が保存されないのである。このように、平均値が保存されない、言い換えれば、加算演算の結果が線形でない場合にはモアレが発生することになる。もしも、マクロに見て「128+128=256」が多い領域があれば、それはモアレの黒い部分であり、そうでない所は比較的明るい部分であるということになる。
ロゲルギストの-モアレが生じる理由は黒さの非線形性による-という言葉はこの「128+128=128、と128+128=256という結果の違いがあり、それがモアレの原因である」ということを示している。
それでは、そのような現象「128+128=128という非線形性」が起きない状態を作ってみる。それには加算の結果である黒がサチらないようにすれば良い。
 |  |  |
 |  |  |
 |  |  |
これでは、いずれの状態でもグレー+グレー=黒、すなわち、64+64=128という風になっている。これは黒がサチっていないからである。すなわち、-モアレが生じる理由である黒さの非線形性さ-がない状態になっている。
それでは、この状態で計算実験Aと同じことをしてみる。それを計算実験Bとする。念のため、計算実験Aをもう一度示す。
 |  |  |
 |  |  |
 |  |  |
| 画像1の黒=0を128にした画像4を平滑化したもの | 画像2の黒=0を128にした画像5を平滑化したもの | 画像4,5を加算したもの |
モアレができていないのがわかるだろうか。これはグレー(128)+グレー(128)=256(もっと黒)で線形な関係が成り立っているからである。平均化された画像で濃度がどこも倍近くになっているのがわかると思う。
モアレのデバイス依存性
LBPではトナーが有る所、すなわち、画像が有る所はほぼ完全に影になる。例え、2枚重ねてもやはり影のままである。しかし、インクジェットならどうだろうか。OHPで使うと、黒といってもLBPに比べて薄い。1枚のOHPの黒よりも、2枚のOHPの黒を重ねた方がかなり黒い。ということは、「黒+黒=もっと黒」と同じである。したがって、OHPを重ね合わせても濃度が保存されている。すなわち、モアレが比較的に出来にくいことになる。ということは、OHPを何で作るかによってモアレの具合が変わることになる。付け加えれば、実際のOHPの場合には透過率を考えなければならない。透過率というものは単なる重ね合わせでない、具体的に言えば、加算演算でなく乗算演算である。それでも、話としては大体は同じことである。
今回はOHPの話に絞ったが、透過原稿でなく反射原稿についても同じである。むしろ、反射原稿の方が乗算演算でなく、加算演算である分、今回の話そのままである。したがって、一般的なモアレについてインク(もしくはそれに相当するもの)の加算演算の具合によって、モアレの発生具合が違うと考えられる。
また、話の単純のために白黒の話に限ったが、カラーのモアレなどについてもほぼ同じであろう。トナーとインク、また、混ざりやすいものと混ざりにくい物の違いなどでも面白い結果が出そうである。TVや液晶のようにほぼ線形の重ね合わせが成り立つであろうものと比較するのも面白そうである。
今回の話を考えている途中で、OHPの重ね合わせと干渉の共通点については、結構奥が深いような気がしてきた。そのため、別の回でもう少し詳しく考えたい。
1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。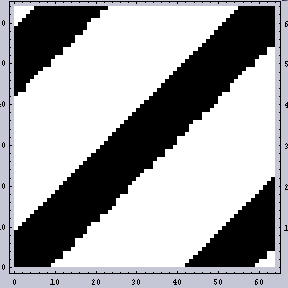 | 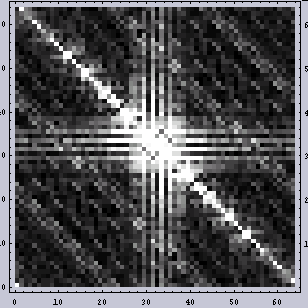 |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる
なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 | 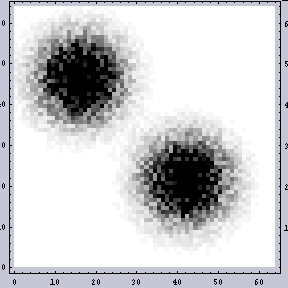 |
 | 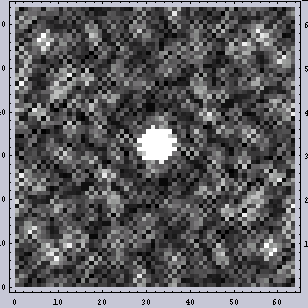 |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
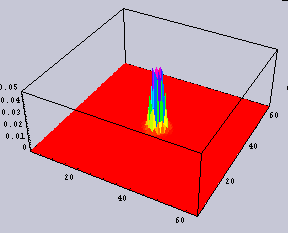 | 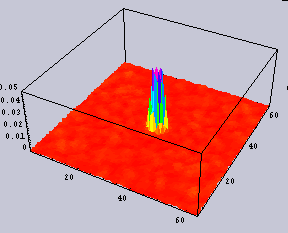 |
 |  |
1999-06-28[n年前へ]
■風呂場の水滴を考える。 
オールヌードの研究員
風呂場の天井から浴槽めがけて、水滴がしたたって音がしているのはよくある風景である。ピーンという(もちろん人によっても印象は違うのだろうが)気持ちのいい音がしている。似たようなものとしては、水琴窟などもある。この音がなぜ鳴るかは、ロゲルギストの「物理の散歩道」に詳しい考察がある。それによれば、水滴が一粒落ちたように見えても、実は何粒かに別れており、ちょうどカルガモの親子のようになっているという。つまり、大きな親の水滴の一粒の後を、何粒かの小さな子どもの水滴が追いかけているという具合である。まず、水滴の親が水面に空洞をつくり、その中に子どもの水滴が飛び込むことにより音が出るという。結局、水滴の音を作っているのは、その子どもの水滴の方だという。「物理の散歩道」の中では、針をつたって水滴を落とせば、子どもの水滴ができないという。
風呂に入って、濡らした手から水滴を落としてみる。指の爪の先から水滴を落とすと音はほとんどしないが、指の「はら」から落とすと派手に音がする。ぜひ、自分でも確かめていただきたい。
爪先は比較的尖っているので、落ちる水滴は一粒だが、比較的平らな指の「はら」からの場合には、カルガモ親子のような水滴が落ちているせいだろう。
なぜ、このような違いが生じるかを推測してみたい。まずは、下の絵を見て欲しい。
 |  |
上の上手な絵が言いたいのは、次のような推測である。
- 平らな表面から水滴が落ちる際には、長く伸びた水のブリッジが出来ていて、1つぶ目の水滴が落ちた後も、このブリッジ部分が「カルガモの子ども」のように小さな水滴となって後を追いかけていくのではないか。
- それに対して、尖った表面から水滴が落ちる際には、先のブリッジ部分のほとんどは水でないため、後続の水滴は発生しない。
計算モデルとしてどのようなものを使うかであるが、私の知っている範囲では大きく分けて2種類のやり方がある。
- 流体をモデル計算する。すなわち、Navier-Stokesの方程式を解く。
- 流体を粒子のようなものの連続体として解く(ex.格子ボルツマン法)
電気通信大学情報工学科情報数理工学講座渡辺研究室( http://assam.im.uec.ac.jp/fluid.html )
 |
また、水滴が水面に衝突する状態の計算は、電気通信大学情報工学科情報数理工学講座渡辺研究室にもあるし、他にもNaSt2DというFreeの2次元Navier-Stokes方程式のソルバーを用いて行われた計算結果が
http://www5.informatik.tu-muenchen.de/forschung/visualisierung/praktikum.html
にある。
 |
Michael Griebel氏らによるNast2Dのコードは公開されているので、その中身をいじりながら、計算を行う予定である。
とりあえず、今回はバックグラウンドを紹介する所までで、次回(といってもすぐではないだろう)に計算の本番に入りたい。
手のひらの実験から考えると、風呂場で水滴の音が聞こえるのは天井が平らなせいだということになる。ならば、鍾乳石のようなつらら形状の天井の風呂場では音がしないのだろうか?しかし、水滴は空気中で落下していく最中には空気の抵抗をうける。そのため、大きな水滴は落ちる最中に分裂し、複数の水滴になってしまう。
となると、
- 落ちる水滴の最初の大きさは、どう決まっているのか。
- 水滴は落下するスピード、水滴の大きさがどの程度になると分裂するのか?
ところで、インクジェット方式のカラープリンターも液滴で画像を描くのだから、液滴の様子は重要な筈である。液滴が飛び散ってしまっては困るし、位置がずれても困る。各社ともカルガモの子ども水滴をなくすために色々工夫をこらしている筈だ。
実は風呂場の水滴問題は重要で、奥が深いのだ。オールヌードで私は考えるのであった。
1999-07-25[n年前へ]
■君はトナーを見たか? 
6umの高速飛行物体
今回の話はミステリー小説のように、「嘘を意識して書きはしないが、本当のことも意識的に書かない」部分がある。お読みの際は注意が必要である。
先日、大手町で開催されていた「JapanHardCopy'99」を見ていた。ちなみに「JapanHardCopy」というのは電子写真装置(複写機やレーザービームプリンター)やインクジェットプリンターなど画像を印字する機械に関する学会である「日本画像学会」が主催するシンポジウムである。その中でも、一番よく「覚えている」発表を考察を含めながら紹介したいと思う。とても「できるかな?」と共通の匂いがするのだ? それに15分の発表がまるまるビデオ(を液晶プロジェクターに表示したもの)によるものというのも珍しいと思う(画面上に時々タイミングを知らせるマーキングが出てはいたが、発表者は喋る長さ調整に苦労していたと思う)。
それは、
現像プロセスにおけるトナー粒子の挙動測定
という発表だ。
この発表は電子写真式の装置の現像装置でトナーが現像される様子を計測した結果の報告である。以前、
ゼロックス写真とセンチメンタルな写真 -コピー機による画像表現について考える - (99.06.06)
の時に電子写真プロセスについて紹介した。今回もその簡単な構成を示しておく。このような機構がコピー機やLBPの内部には入っているのだ。(ドラム表面の画としてはRicohのWEBがわかりやすい。)
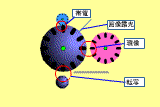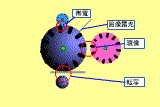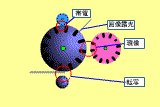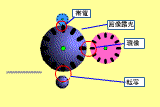 |
上の概略図で現像装置は右の薄紫の円である。感光ドラムが中央の大きな円だ。この発表は、現像装置と感光ドラムの近接部(画面中央のの赤丸で囲まれた部分)で何が起きているかを測定しているのだ。
しかし、全ての現像装置ではなく現像装置と感光ドラムが非接触のタイプのものに関する報告である。現像装置から感光ドラムへトナーを現像させてやるわけだが、両者が非接触であるということはトナー粒子を現像装置から飛ばしてやることにより現像させるわけである。高電界を印加して電気的な力によりトナー粒子を飛翔させるのだ。そのような場合にトナー粒子がどのような挙動を示しているかを計測しているのである。
現像装置と感光ドラムの間の距離というのは通常300um程度である。また、最近のトナーの粒径は6um程度である。300umのギャップ中を6um程度の飛行物体が数多く飛びまくるのである。数多くといってもピンとこないかもしれないので、数値的な考察をしてみる。1cm^2(1平方センチメートル)の黒い四角を印刷するのにトナー粒子はどのていど必要だろうか。もしトナー1個が10um角の領域を完全に覆えるならトナーが1000x1000個あれば1cm^2の区画を完全に覆えるだろう。しかし、現実問題として1層だけでは覆えるわけがないので仮に5層必要だとすると、5x10^6個のトナーが1cm^2(1平方センチメートル)の黒い四角を印刷するのに使われていることになる。500万個である。
その数多いトナー粒子が飛行しているものの中から1個単位のトナー粒子を計測しどのような飛行をしているかを調べているのだ。数100um角の領域中で数百万個のトナーが飛行する中から1個のトナー粒子を調べるのである。まるで、大都会で一人の人の追跡取材し、その人にライトをあてるような作業ではないか。ロマンチックとは思えないだろうか?
それでは、どのように飛行しているかを予稿集の図から抜き出してみよう。
 |
この写真中では画面上のドラムと現像装置は500um離れている。また、上と下の写真ではトナーを飛行させるための電界の波形が異なる。上が単純な矩形波であり、下が矩形波の正と負の電界がかかる時間長さが異なるものである。まるでトナー粒子の動きが物理的なオシロスコープのようである。
これはほぼ1/15秒間の軌跡であり、予稿集の写真から推定するに、その間に7cm程度は移動している。ということはトナー粒子は1秒間に1m程度は移動していることになる。秒速1mである。しかも方向を鋭く変えながらであるから、加速度としては凄いものがあるし、瞬間の最大速度もはるかにこれより速いだろう。
普段LBPなどで出力をすることも多いと思うが、その出力画像を形成しているトナー粒子たちがこんなに高速でアクロバット飛行してきたとは知らなかった人も多いだろう。この写真自体は今回の発表の導入部分に過ぎなく、本題がこの後に続くのだが、結構面白い写真ではないだろうか。トナー粒子の動きが一目瞭然である。
ところで、ここまできても「おまえの考察が少なすぎるぞ。」と言われる方はいらっしゃらないですよね。「これ、おまえの発表じゃないか。自作自演じゃないか。」とおっしゃる方はいるでしょうけど。
1999-09-17[n年前へ]
■モアレ、デバイス、2項分布の三題話 
淡色インクの副作用
今回は、9ヶ月間も寝かせた伏線にまつわる話である。いや、別に寝かせるつもりは無かったのだが、いつのまにかそんなに時間が経ってしまった。
以前、
という話があったが、その2つを結びつけるミッシングリンクについて考えてみたいと思う。「2項分布のムラについて考える(1999.01.08)」の最後に「今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、続く...」と書いた。「その続き」というわけである。始めに「2項分布のムラについて考える(1999.01.08)」の要点をまとめると以下のようになる。それは、
- ランダムと呼ばれるものの内で代表的な2項分布においては、当然のごとく「ある領域での平均値はばらつく」。
- そして、そのばらつきは直感的に考える程度よりももっとばらつく。
- 例えば、2値画像で考えるならば、2048dpi程度の解像度でランダムなデータを並べた場合には、人間の目はざらつきを感じてしまう。
そして、「モアレはデバイスに依存するか?(1998.11.20)」での要点は
- モアレにはデバイス依存性がある
- 線形な重ね合わせが成り立たない場合にはモアレが発生する。
最近のインクジェットプリンターはCMYKの4色インクだけでなく、淡色インクも使うものもある。淡色のインクを使うことで階調豊かな画像を印字できるわけだ。4色インクだけではディザなどを使って、解像度を下げて階調を出さなければならないわけであるが、それが不要になるわけだ。
解像度を下げないですむわけであるから、ディザのざらつきを感じないですむわけだ。しかし、淡色のインクを使った場合の効果というのはそれだけではないように思われる。HP(ヒューレッドパッカード)などのWEBのプリンター紹介を読んでいると、「淡色のインクを重ねて濃度を出す」というような記述を目にする。これは「少なくとも淡色インクでは線形性(あるいはそれに近い関係)が成り立つ」ということだ。
インクジェットプリンターの解像度を上げたときに、インク滴が意図しないところへずれてしまうことはきっとあるだろう。その際に他のインク滴と重なったらどうなるだろうか?意図しなくても他のインク滴との重ね合わせは発生してしまうだろう。
重ね合わせが成り立たない、非線型なインクではモアレが発生する。言いかえれば、意図しない濃度のばらつき・ざらつきが発生してしまう。「2項分布のムラについて考える(1999.01.08)」で考えたようにランダムに重ね合わさるから広い領域では一定だろうというのは予想外に成り立たないのである。でたらめというのは私の予想外に大きく効いてくるのである。
しかし、重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しないことになる。参考までにインクジェットの印字画像の拡大写真を示してみる。
 |  |
「重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しない」と、書いただけでは意図するところが伝わらないと思うので、「モアレはデバイスに依存するか?(1998.11.20)」で使った画像を用いて考えてみる。この画像は重ね合わせがある幾何学模様で生じているが、この現象がランダムに起こっているものとして読み替えて欲しい。
 |  |  |
下は、淡色のインクで重ね合わせ(インク滴の意図しない重なり)が生じた場合である。
 |  |  |
なんの模様も生じていなく、意図した通りの画像出力ができているのがわかると思う。
ということで、今回の話(というか前の2回の話)の繋がりは、
淡色のインクを用いたインクジェットプリンターでは、意図しないインク滴の重ね合わせが生じてしまっても、濃度変化が生じにくく、意図しないインク滴の重ね合わせがでたらめに発生してしまったとしても、画像にはあらわれない可能性があるということである。
うーん、マニアックな内容だ。「身近な疑問を調べる」という看板に偽り有り、である。しかも単なる推論だ。
しかし、もしもインクジェットプリンターを買う人がいるならば、淡色のインクを使っているものを購入するといいかもしれない、ということがわかっただけでも良しとしておこう。