1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A | B | C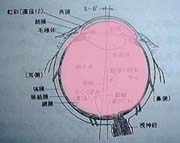 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
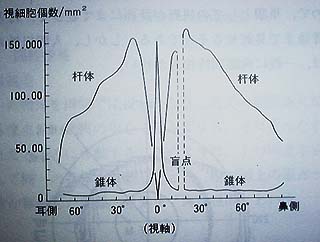 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
2003-03-22[n年前へ]
■ファミコンの謎の一つが今明らかに 
 色々なシミュレーターを見かけることもあるし、自分で作ることもある。が、このシミュレーションというかエミュレーションには「目から鱗」だったのである。というわけで、その「目から鱗」のエミュレーションがこの「ファミコン"カセットずらし"をエミュレートしてみる」
色々なシミュレーターを見かけることもあるし、自分で作ることもある。が、このシミュレーションというかエミュレーションには「目から鱗」だったのである。というわけで、その「目から鱗」のエミュレーションがこの「ファミコン"カセットずらし"をエミュレートしてみる」
「電源が入ったままのファミコン本体からカセットを少しだけ引き抜いて、マリオを地中奥深くに落としたり、見えていないはずの金塊の場所が判ったり、ドラクエでまだ行ったことのない場所に移動できたり…」といったナゾの発生過程を実証したモノなのである。素晴らしいのだ。
2003-09-05[n年前へ]
2003-09-06[n年前へ]
■Elasticity Simulatorで眺める「オッパイ星人のヤング率」 
どうせなら面白く物理を眺めれば、きっと中高生(大学生も?)科学を好きになるだろうということで、どうせならElasticity Simulatorで「オッパイのヤング率」を眺めてみることにしよう。
まずは、このJava Appletから 1."shape"から"disk"を選択する
2.真ん中の点を全て右クリックして、固定点(大きい丸)に変更する
3."triangular mesh"にチェックを入れる
4."gravity"にチェックを入れる
という順番の作業をする。すると、こんな画面になる。
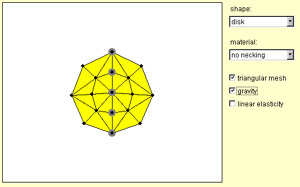
固定点を作成したことでこのモデルは左右対称になったわけで、(例えば)左半分を無視して眺めてみることができる。つまり、こんな風に「半球状に」眺めることができる。
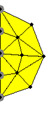
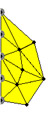
ハイ、判りましたでしょうか?つまり、このElasticity Simulatorは「オッパイ・シミュレータ」に大変身するわけです。"material"を変えて、ヤング率を変えることで「堅いオッパイ」「柔らかいオッパイ」、「ヤングなオッパイ」「アダルトなオッパイ」などさまざまな物理実験をすることができるようになります。もちろん、無重力条件下とか動的特性なども眺めることができるのです。
これで、きっと物理大好きな中高生ができあがり、です。少し動機がヘンかもしれませんが、とりあえず弾性体物理学(それともオッパイ)が大好きになるハズです。というわけで、こんな「物理講座」に対する中高生を持つPTAのご意見などを少しばかり聴いてみたいところですねー。感謝の声か、非難の声か、さてさてどちらでしょうねぇ。
2003-10-11[n年前へ]
■BMLwalker 
とてもシンプルな「歩行シミュレータ」 左上のスライダで性別の具合や落ち着きや楽しさの度合いを変えてみると面白い。シンプルな点や線から伝わってくる「落ち着きや楽しさや性差」を感じることで、それらがいったい何であるかすら考えさせてくれる。