hirax.net::Keywords::「トリック」のブログ

■OHPによるモアレと光の干渉の相似について考える。　　

ヒラックス・ディザの提案

「位相保存ディザマトリックス」

4x1ドットからなるマトリックス

　この「黒、黒、白、白」というパターンを次の図と見比べる。

位相遅れ0の矩形波、(4つに分割すると、「黒、黒、白、白」となる)

4x1ドットのマトリックスで各位相の矩形波を表現した例1

「モアレのデバイス依存について考える。」で行ったようにこのようなパターンをOHPで打ち出し、重ね合わせてみる。例えば、位相0と位相180のものを重ね合わせたらどうなるだろうか。4x1ドットのマトリックスの全てが黒になる。すなわち、真っ黒になるのがわかるだろう。それでは、位相0と位相90のものではどうだろうか。4x1ドットのマトリックスの内、3ドットが黒、1ドットが白である。位相が同じものどうしを重ね合わせると、元と同じく、2ドットが黒、2ドットが白である。
　ということは、「位相が同じ物どうしであれば、元の明るさを保持する」、「位相が逆であれば真っ黒になる」、「位相が少しずれているのあれば、明るさはその分少し暗くなる」という性質があることがわかる。光の干渉の場合とほとんど同じ性質を持っているのがわかると思う。違うのは、同じ位相のものどうしが重ね合わさった時に、重ね合わせた分明るさが2倍になるか、そうでなくてそのままなのかという違いだけである。
　つまり、この4x1ドットのマトリックスは「きちんと演算が成立する位相情報が記録されている」ということになる。そして、位相が異なるものを重ね合わせた時の位相情報の保存までも考えてやるならば、先ほどの例1は次のように位相の定義を変えてやるほうがいいと思う。

各矩形波の黒の中心位置として位相の値を定義し、4x1ドットのマトリックスで各位相の矩形波を表現した例2

　この例2では位相の数字は各矩形波の中心位置を現すことにしている。それでは、この定義を用いて、位相90,180のものを足しあわせたらどうなるだろうか。下に示すのがその結果である。

例2の定義を用いて位相90,180を足しあわせると

　位相90と位相180のものを足しあわせると、波形はブロードになり、中心すなわち位相135のものができているのがわかる。また、明るさはこれまでが、2/4だったものが1/4であることになり、強度も弱まっているのが表現されている。

　つまり、このようなマトリックスによる表現は波の持つ位相と強度と波形を表現し、演算も成り立っていることがわかる。それでは、例2の基本マトリックスが縦方向に繰り返されている画像(1(基本マトリックス)x8ピクセル)を考える。こんな感じである。

例2が繰り返されているもの

　これは下方向から進行している矩形波の様子そのままである。なお、この図でも基本となるマトリックスは4x1ドットであるから、この例では要素としては1x8ピクセルを示しているのである。どの要素も振幅(強度)自体は同じである。平均の明るさは同じである、と言い換えても良い。また、波形自体も同じである。しかし、位相が異なっている。波の進行そのままである。

さらに強度情報を加える

4x4ドットのマトリックスで強度の快調を表現した例A

4x4ドットのマトリックスで強度の階調を表現した例B

　このような「位相、波形、強度情報を保存し、演算も成立する」マトリックス表現を仮に「HiraxDither(ヒラックス・ディザ)」と呼ぼう。先の「モアレのデバイス依存について考える。」で使ったスペックルパターンの例はこのヒラックス・ディザの簡易なもの(2x1基本マトリックスのもの)を使っていた。
　また、「モアレのデバイス依存について考える。」で使った同心円状の画像のモアレのパターンは実はヒラックスパターンの特殊な例(1x1基本マトリックスのもの)を用いていたのである。そこでは、単に位相情報しか記憶されていない。この場合には、白、黒が位相情報を現していたのである。だから、黒、黒どうしの所(すなわち、位相が同じ所)では平均の明るさは変化せず、黒、白が重なった部分(すなわち、位相が反対である所)でのみ打ち消し合い、暗くなっていたわけである。波形も、強度情報もこの場合には記録されていない。

「ヒラックス・ディザ」とホログラフィーの相似点

　また、もう少し深く考えると、もっと他の分野とも繋がるかもしれない。いずれ、また考えてみたい。

■立体音感を考える　

バーチャルサウンドソフトウェアを作ってみよう

　立体感というものには何故か強く心惹かれるものがある。まして、それが人工的な立体感であるならば、なおさらである。それは、画像・映像であっても、音であっても同じだ。色覚なども同様なのだが、人間の感覚というものを人間自身の技術により再現できたりするのが、実に面白い。

　何より、自分が実感できるというのが良い。結果を自分で感じることができるというのは、素晴らしいと思う。よくソフト技術者などで、「もう少し目に見えるものが作りたい」という人がいるが、それと同じである。

　小・中学校などでも実感できる教材や授業というのがあれば素晴らしいと思う。最近のWEBを眺めていると、そういう先生方のグループも多いようだ。そういう先生は「えらいなぁ」とつくづく思う。今の学校の先生は、そういうことをすればするほど、仕事としては時間単価が下がってしまうのだろう。それでも、そういった先生方は、きっとそういうことは気にしてはいられないのだろう。ホントにエライ。

　さて、立体感を実現するソフトであるが、そういった技術には色々なモノがある。音響の立体感の実現を目指す技術に関しても、古くから数多い技術がある。そういったものを追求しているWEBも多々あり、
　「今日の必ずトクする一言(http://www.tomoya.com/)」の

• 山本式スーパーバイノーラルコンペンセーターのナゾ(その２、ソースを考える編)
• http://www.bekkoame.ne.jp/~jh6bha/higa9810.html#981013
• 山本式スーパーバイノーラルコンペンセーターのナゾ
• http://www.bekkoame.ne.jp/~jh6bha/higa9810.html#981008
• 山本式バーチャルサウンドシステムのナゾその２(原理解説編)
• http://www.bekkoame.ne.jp/~jh6bha/higa9804.html#980421
• 山本式バーチャルサウンドシステム(PATPEND.)のナゾ
• http://www.bekkoame.ne.jp/~jh6bha/higa9803.html#980307

　また、そういったものを実現しようとする製品は昔から掃いて捨てるほどある。最近の製品では、

• ヤマハ、スピーカー間隔0でステレオ音場を実現するLSI
• http://www.watch.impress.co.jp/pc/docs/article/990122/yamaha.htm
• ヤマハ デジタルオーディオ用LSI『YSS901』
• http://www.yamaha.co.jp/news/99012101.html

　私も出張などで新幹線などに乗っている際には、E-500などでヘッドホンで音楽を聴いていることが多い。そういう時には、先の「山本式スーパーバイノーラルコンペンセーター」などが欲しくなり、音の立体感などについて色々と考えてしまう。必要に迫られているせいか、立体音感については、私もとても興味を惹かれるのである。
　というわけで、「できるかな?」でも立体音響について考えてみたいと思う。といっても、考えるだけでは面白くない。それに「ナントカの考え休むに至り」ともいう。私が考えるだけでは、何にもならないし、しょうがない。色々と実験をして遊んでみたい。
　そのために、まずはいくつかの道具を作ってみることにした。

　今回、作成するのは、山本式バーチャルサウンドシステムソフトウェア(名付けてYVSSS。略称が長いので、以降YVS3と称することにする。)である。先の「今日の必ずトクする一言(http://www.tomoya.com/)」の一連の話しに出てくるそれである。スピーカーマトリックスの程度を小さくしたものである。

　バーチャルサウンドシステムソフトウェアというと仰々しいし、ものすごいソフトウェアに思えるかもしれないが、実はそんな大したモノではない。それどころか、実に簡単なモノである。実際には、Waveファイルを開いて、そのファイルの左チャンネル(L)、右チャンネル(R)に対して、

• R'＝ R - 1/3L
• L'＝ L - 1/3R

　ここに、今回作成したソフトを置いておく。いつものことであるが、完成度はアルファ版以下である。

• wavemixpro.lzh 444kB

　使い方を示しておく。まず、下が動作画面である。水平方向にスライダーがあるが、チャンネル同士の演算の係数を決めるものである。左端が0%であり、右端が100%である。

WaveMixPro(YVS3)の動作画面

　すなわち、スライダーが左端であれば、

• R'＝ R - 0 L = R
• L'＝ L- 0 R = L

• R'＝ R - L
• L'＝ L- R

　　さて、このソフトを使って、

• 種ともこのアルバム「感傷」から「はい、チーズ!」
• THE POLICEのLive at the "Omni" Atlanta, Georgia During 1983 U.S.A Tourから"SoLonely"

　試聴のやりかたは、Cd2wav32.exeを使い、CDからWAVファイルにする。そして、WaveMixPro(YVS3)を使って、バーチャルサウンドシステム構築する。そして、それをヘッドホーンで試聴するわけだ。適当にチャンネル同士の演算の係数を変化させ、聴いてみた。果たして、立体感は増しているか?

　さて、試聴した結果であるが、「うーん。」という感じだ。
　係数を大きくすると、まるで「カラオケ製造器」である。ボーカルが消えるだけである。しかも、聴衆が頭の真ん中に居座っているような感じである。つまり、立体感がむしろなくなってしまっている。「何故、オマエらはオレの頭の真ん中で拍手をするのだ」、と言いたくなる。頭が変になりそうである。
　かといって、小さいとよく違いがわからない。困ったものである。

　さてさて、まだまだ第一回目ではあるが、前途多難の気配であるのが心配なところだ。

■モアレがタネの科学のふろく　

うれし、懐かし、学研の科学

　先日、友人夫妻で面白いものを見せてもらった。そこで、すかさずオネダリをして手に入れてきた。それが下の写真のものである。
 

6年の科学　1998年1号　トリックトランプ「マル秘」超魔術13

　これは学研の科学の学習教材である。「科学の学習教材」というよりは、「科学のふろく」といった方が通りが良いかもしれない。この写真のものは「6年の科学　1998年1号　トリックトランプ「マル秘」超魔術13」である。これを私にくれた友人(妻の方)は「学研教室」の「先生」をやっているので、こういう面白いものを持っているのである。

　残念ながら、付録の一部だけで、中身が全部揃っているわけではない。それに加えて、本誌もない。そこで、手元にある材料からトランプトリックを想像しなければならない。しかし、その想像しなければならないところが、また面白いのである。手品の「タネ」を想像し、実際に検証できるのだから、楽しくないわけがない。

　こういう理系心をくすぐる、懐かしいものというのは色々ある。以前登場した、学研の電子ブロックもそうであるし、雑誌の「子供の科学」もそうだ。そういった中でも、この学研の科学のふろく(学習教材)はその最たるものだろう。こういった、科学の付録は学研のサイト内の

• 科学の付録　(http://kids.gakken.co.jp/kagaku/furoku/index.html )

　さて、今回の「6年の科学　1998年1号　トリックトランプ「マル秘」超魔術13」のネタ探しをしていると、面白いものを見つけた。それが下の写真である。何にも書いてないトランプに半透明シートをかけると、アラ不思議、ハートの5が現れるのである。
 

何にも書いてないトランプに半透明シートをかけるとアラ不思議
ハートの5が現れる

　この「魔法のトランプ」のタネはもちろん「アレ」だ。「できるかな?」にもよく登場してきた「モアレ」である。これまで、

• モアレはデバイスに依存するか？(1998.11.20)
• OHPによるモアレと光の干渉の相似について考える。　-ヒラックス・ディザの提案 -　(1998.11.22)
• モアレ、デバイス、2項分布の三題話- 淡色インクの副作用 - (1999.09.17)

　このトランプの表面の模様を拡大してみるとこんな感じになる。これは「ハートの先端部分の拡大写真」だ。赤い線によるハーフトーンパターンが変化している部分(実はハートマークの先端部分)があるのがわかる。この模様は結構細かく、400線/inchくらいである。
 

ハートの先端部分の拡大写真

　このようなトランプに、黒い斜線が描かれた半透明シートをかぶせると、モアレが発生して模様が見えるわけである。下の写真が、トランプに半透明シートをかぶせたところである。半透明シートには実は黒い斜線模様が描かれていることがわかる。
 

このようなトランプに、
黒い斜線が描かれた半透明シートをかぶせると、
モアレが発生して模様が見える

　そして、トランプの模様と半透明シートの模様の間でモアレが発生して、その結果として「5」
の文字が浮かび上がっているのがわかると思う。

　このトランプのタネのような画像を自分でも適当に作ってみることにする。やり方はとても簡単である。ハーフトーン模様を作成して、模様を書いて、模様部分だけハーフトーンを変化させてやればいいだけである。そして、元のハーフトーンと重ね合わせてやれば、模様が浮き上がるのである。こういう細工をしないと読めない画像を使って、何か面白いことをできるかもしれない。
 

同じような画像の例

A　ハーフトーンを作成する

B　模様を書いて、模様部分だけハーフトーンを変化させてやる

C　AとBを重ね合わせるとアラ不思議(子供にとってはね)

　一応、モアレはデバイスに依存するか？(1998.11.20)の時のように今回も二つの画像の重ね合わせの時に、線形性が成り立つ場合と、成り立たない場合の比較をしておく。
 

上の画像の重ねあわせにおいて、線形性が成り立つ場合と成り立たない場合の比較

線形性が成り立つようにして 先のAとBを重ね合わせてみたもの

上の画像を平滑化したもの 線形性が成り立つ場合には、モアレが発生していないのがわかる

ちなみにこれが先のCを平滑化したもの つまり、非線形性を持つ場合 この場合にはモアレが発生する

　今回の場合も当然、線形性が成り立つ場合にはモアレが発生しないのがわかると思う。今回のトランプ手品も、半透明シートとトランプの模様の間の重ね合わせの非線形性を利用していたわけである。
　この線形性と非線形性の重ね合わせの違いも利用してみれば、もっと新しい何か面白い手品やおもちゃのネタになるかもしれない。インクジェットプリンターの淡色インクと、濃いインクの違いを利用して何か面白いトリックはできないだろうか？

　さて、先の知人夫妻は共に「先生」である。なので、時折子供に「どうやって教えるか」という話になることがある。子供という「タネ」をどうやって育てていくか、という話である。子どもが人から言われたことでなく、自分で調べて何かを覚えるにはどうしたら良いか、などだ。もちろん、それは「先生」もまた同じである。人に言われたことを鵜呑みにするのではなく、自分で「実感する」のはむしろ子どもより「先生」の方が難しいかもしれない。

　私も先日あるメーリングリストで

「先々」のある（製造業に携わる）子ども・青年などわずかでしょう

■レトリック用語・用例集　

続　今日の参考サイト。（リンク）

■草枕で遊ぶ　

それが人間の科学なんだよ、と誰かが言った

　どうしても割り切らないではいられない話だと知った時、それが人間の科学なんだよ、と...(半神)

　私が大好きな演劇の一つに「半神」がある。レイ・ブラッドベリ・萩尾望都・野田秀樹の共作とも言うべきこの「半神」の中で1/2+ 1/2 = 2/4 という「螺旋方程式」の謎に対して

「その謎はひとごと(他人事)ではない。」
「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」

　ところで野田秀樹ほど言葉遊びが巧みな人もそうそういないだろうが、この

「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」

　智に働けば角が立つ。情に棹させば流される。意地を通せば窮屈だ。とかくに人の世は住みにくい。人の世を作ったものは神でもなければ鬼でもない。やはり向う三軒両隣りにちらちらするただの人である。ただの人が作った人の世が住みにくいからとて、越す国はあるまい。あれば人でなしの国へ行くばかりだ。人でなしの国は人の世よりもなお住みにくかろう。

　この

「人の世が住みにくい」
->「人が作った世が住みにくいならば、人でないものの世なら住みやすいだろうか」
-> 「人でなしの国へ行くばかり」
-> 「人でなしの国は人の世よりもなお住みにくい」

　ところで、以前

• 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)

「漱石とあたたかな科学」小山慶太著 講談社学術文庫

　花は科学じゃない、しかし植物学は科学である。鳥は科学じゃない、しかし動物学は科学である。文学はもとより科学じゃない、しかし文学の批評または歴史は科学である。

「文学のどこに観察、実験、数理解析が施せるのであろうか。」

　「草枕」は青年画家がブラブラしたり、ボうっと色々なことを考えたりする話だ。そして、いかに芸術が生まれるかということに考えてみたりするのである。例えば、冒頭では

　住みにくさが高じると、安い所へ引き越したくなる。どこへ越しても住みにくいと悟った時、詩が生れて、画が出来る。

して見ると四角な世界から常識と名のつく、一角を磨滅して、三角のうちに住むのを芸術家と呼んでもよかろう。

　一体、青年画家がどんな時に「画」を書くのかどうかを知るために、他の単語の出現分布と「画」の出現分布を調べてみることにした。今回、ノミネートしてみた単語は「角」・「男」・「女」である。

　角が立つ四角い人の世の中で三角のうちに住むのが芸術家であるならば、その「角」と「画」の相関は調べてみたいと思うハズである。また、これまでに様々な「男」と「女」の関係を考えてきた「できるかな?」であるから、やはりここは「男」と「女」もノミネートしないわけにはいかないだろう。

　そこで、「画」・「角」・「男」・「女」の各語の出現分布を調べてみたのが次の各図である。もちろん、今回も前回

• 六の宮の姫君 - さがし続けても、見つからない- (2000.08.30)

「画」・「角」・「男」・「女」の各語の出現分布

「画」	「角」
「男」	「女」

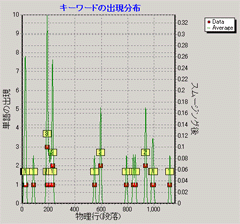　次に、「画」の出現分布に対するそれぞれの言葉の出現分布の相関値を計算してみよう(なお、計算の安定のために、適当な平滑化をここでは行っている。)主人公の青年画家がどんな時に「画」について考えたり、描こうとしたりするかを考えてみるわけである。その計算結果が次の表である。
 

　そして、さらにこれをグラフにしてみたものが、下のグラフである。
 

「画」の出現分布に対するそれぞれの言葉の出現分布の相関値のグラフ

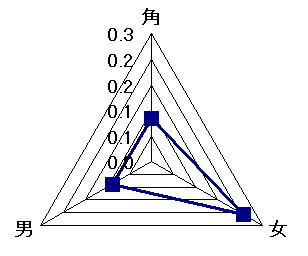　おやおや、困ったなぁ。ちょっと、この「画」と「女」の相関の高さはちょっと異常だなぁ。「角」や「男」の出現分布の「画」に対する相関は0.1以下であるが、何と「女」は0.2を越えている。最初は、「画」と「角」を強引に結びつけて話を終わらせるつもりでいたのになぁ。これじゃぁ、主人公はヒロインを前にするときだけ芸術家になるみたいじゃないの。おかしいなぁ、こんな狙いじゃなかったのになぁ...まるで、「草枕」は漱石の前田卓へのラブレターみたいに思えてきてしまうではありませんか...
　う〜ん、これはどっか間違えたかなぁ。まぁ、いいや。今日はもう眠いし。
 

　ところで、「草枕」ではどのようにして文学・音楽・絵画などのさまざまな芸術が生まれて来るかが書かれている。そして、冒頭の「半神」でも、シャム双生児の姉妹とともに「螺旋方程式」の謎を追いかけるうちに、人の心を動かす孤独と音が生まれてくるようすが語られていく。
 

孤独は、ヒトになる子にあげよう。代わりに、おまえには音をつくってあげよう。
( 夢の遊眠社　半神 )

　今回の相関解析では、「芸術は女を前にしたときに生まれる」というフザケタ結果に終わってしまったが、その真偽についてはまたいつか考えてみることにして、とりあえず今回は草枕の中の台詞で話を強引に終わらせたいと思う。
 

　越す事のならぬ世が住みにくければ、住みにくい所をどれほどか、寛容て、束の間の命を、束の間でも住みよくせねばならぬ。ここに詩人という天職が出来て、ここに画家という使命が降る。あらゆる芸術の士は人の世を長閑にし、人の心を豊かにするが故に尊とい。