2001-08-07[n年前へ]
■「ボケ」た背景で包み込め 
デジカメ画像をキレイにボカそう アルゴリズム編
最近、新しいデジカメを物色中である。私はこれまではFinePix4700zを使っていたのだけど、そのFinePixが半年程度で壊れてしまった。というわけで、C-4040ZOOMがどんなものか期待しているところである。
壊れたFinePixと言えば、そもそも壊れたFinePixは一台ではなかった。私はすでにFinePixを二台も買っているのだ。そして、もうすでに二台とも壊れてしまっているのである。連続殺人事件ならぬ、連続カメラ自殺事件なのである。
まず、一台目に買ったFinePix700ははメキシコのティファナでポケットから落としたら、バッテリーから電源が供給されなくなった。もちろん、ACアダプターを使えば立派に動くのだけれど、それでは少しばかり機動性に欠けてしまう。まさか発電機を持ち歩くわけにはいかないし、コンセントの近くでしか撮影することができないとなると、それは非常に困ってしまう。そこで、すかさず二代目としてFinePix4700zを私は買った。ところが、買ってから半年位たったある日、今度は勤務先の駐車場でポケットから落としてしまった。すると、今度はファインダー視野がズームに連動しなくなって、なおかつレンズがまるでジョイスティックのようにあらゆる方向に曲がるようになってしまった。
こんな風にデジカメはとっても壊れやすくて、半年毎にデジカメ出費を強いられる私に周囲は「落としたオマエが悪い」と非常に冷たいのである。残念なのだ。「そういうのは壊れたんじゃなくて、壊したんだ」と被害者である私をまるで加害者のように告発する人さえいるのである。連続カメラ自殺事件は実は他殺で、しかも犯人は私だと告発する輩さえいるのだ。ひどい話である。
ところで、C-4040に期待しているのは、コンパクトで、レンズアダプターが使えて、レンズがF1.8と明るいことなのである。コンパクトなのは持ち歩くために必要だし、私はなんと言っても超広角デジカメが欲しいのだが、そんなデジカメはないので、ワイドコンバーターを付けたいのでレンズアダプターが必要なのである。明るいレンズの方は、うす暗い中でも撮影する時に重宝しそうなので、少し期待しているのである。
ところで、この位明るいレンズであれば、もう少しぼかすことができるものだろうか?デジカメで写真を撮ってもどうしてもボケない。35mmフィルムを使っているカメラなどと比べるともう全然ボケない。もうほんとにボケない。
例えば、35mmカメラで135mm F4.5開放のレンズなら、ピントの合ってない背景はこの位はボケる。これは京都の哲学の道近くにある吉田山で撮った写真だ。
 |  |
ピントが合っている位置以外は光がボケて、キレイなボケが発生する。どちらの写真も絞りは開放で撮影しているので、後ろの風景はほぼ丸くボケている。ぼかせばキレイというわけではないけれど、背景などがごちゃごちゃしている中で対象物だけを浮き上がらせたい場合には、「ボケ」させるととても良い感じになる。
しかし、デジカメではそうそう簡単にボケた画像を撮影することはできない。35mmフィルムに比べて、CCDサイズが小さいからである。35mmカメラよりAPSカメラはもっとぼけなくて、それよりデジカメはさらにボケないのである。そんな様子を見るために、二台目として買ったFinePix4700zで「ボケ」を意識して撮影してみたものが下の写真である。手前の植物にピントが合って、奥の道の先はボケてはいるのだけれど、それでも先程の写真などとは比べものにならないほどわずかしかボケていない。
 |
ところで、このような画像の「ボケ」を考えるとき、「ボケ」た画像をシャープに復元しようという話は非常にポピュラーな話題である。例えば、本「できるかな?」でもこれまでに
といった感じで遊んできた。また、さらには「恋の形」を復元しようとしたとか、このようなアプローチを遥か昔に考えていた漱石の「文学論」を振り返ってみたりしたきたのである。しかし、これらはいずれも「ボケたデータを復元する」という問題であった。一方、この逆のアプローチである「シャープなデータをボケたデータにする」という問題も結構ポピュラーである。例えば、音楽をホールやライブハウス風にボケた音にするDSPはかなりの数のオーディオ装置に付けられている。これも、もともとはシャープな音声データが部屋の中でボケていく様子をシミュレートする回路である。また、画像に関する話題でも、ピント位置をずらした複数の画像から任意の「ボケ」画像を作成するといった話題もたまに見かける。
そこで、「できるかな?」でもデジカメ画像を35mmカメラ風にキレイにぼかすことに挑戦してみることにした。今回は、まずはアルゴリズムを確認して、次回以降で簡単プログラムを作成してみることにしたい。
まずは、似たようなソフトウェアがあるかどうか、Googleで適当なキーワードを使って検索をかけてみると、IrisFilter(http://www.reiji.net/iris/)というソフトウェアがあった。これは、「写真のぴんぼけを再現する」というフィルターだった。サンプル写真などを見てみると、これがなかなかきれいだった。例えば、早朝の御殿場の路上を「在りし日のFinePix4700z」で撮影した写真にこのフィルタをかけて、「ボケ」を加えてみたのが下の画像である。
 |  |
ここではこんな![]() 六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
六角形の絞り形状をを用いてみた。右の処理画像中の、車のテールランプや車の下部を眺めてみると、鋭いハイライト部が六角形に光っているのがわかだろう。確かに、「ボケ」がカメラの絞り形状になっていて、良い感じである。
WEBページの記載によれば、このIris Filterは「フィルム特性曲線を利用し、レンズから通った光がフィルムを感光させる様子を再現しています」ということである。なんでも、特許も国内・USP共に出願済みということだが、特願2000-100042もU.S.PTO 09/772532も未だ公開にはなっていないようで、残念ながら特許の内容を読むことはできなない。
このWEBページの記述の中で面白いのは、「データ上の数値をそのまま拡散させる従来のPhotoshopをはじめとした画像処理ソフトと違い、実際のフィルムに当たる光の量(露光量)を逆算し、その露光量をもってピントがずれている様子を再現します」という歌い文句でPhotoshopの「ガウスぼかし」と比較広告してある部分である。
試しに、先の画像をIris Filterで「ボケ」を加えた画像と、Photoshopの「ガウスぼかし」とで「ボケ」を加えた画像を比較してみると、下の二枚の画像のようになる。確かにIrisFilterの売り文句通り、こうして比較してみるとPhotoshopガウスぼかしが写真の「ボケ」っぽくないのに対して、IrisFilterの「ボケ」が写真のそれっぽいことが良くわかる。
 |  |
さて、お仕着せのソフトを使ってみるだけではなくて、自分でデジカメ画像をキレイに「ボケ」させてみることにしたい。というわけで、hirax.net風「ボケ」フィルターの動作を考えてみる。
まずは、毎度のことだがオリジナル画像が「ボケ」る様子を計算する式は
逆フーリエ変換( フーリエ変換( オリジナル画像 ) x フーリエ変換(ボケ具合 ) )と表すことができる。詳しくは、「宇宙人はどこにいる?」の回でも読んでもらうことにして、簡単に言えば周波数領域でオリジナル画像とボケ具合を掛け算をしさえすれば良いのである。つまり、今回のデジカメ画像をぼかす場合だったら、
- デジカメ画像と「ボケ」具合をそれぞれフーリエ変換し周波数空間に変換
- 周波数空間で乗算を行う
- 逆フーリエ変換して実空間に戻す
じゃぁ、早速やってみようとなるわけだが、その前にもう一つ注意することがある。それは、RGB画像の数値というものは実は元々「明るさを対数変換した値」であるということなのである。人間の目も含めて世の中の大抵の材料は対数的な感度を持っている。例えば、人間の目に「2倍明るい」という場合に、光は「2倍明るい」というわけではない。その場合には指数的にX^2倍明るいのである(ここで、xの値はそれぞれのデバイスによって色々と違う)。その明るさをRGB画像の数値データにする時に、明るさの対数をとってLog[x,X^2]で2という数値として表しているわけだ。
RGB画像の数値が「明るさを対数変換した値」だというようすの一例を示すと下の図のようになる。
横軸 = 0〜255の数値データ 縦軸 = エネルギー 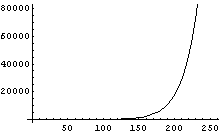 | 横軸 = 0〜255の数値データ 縦軸 = エネルギー  |
逆に明るさからRGB画像の数値データへの変換グラフは例えばこんな感じである。RGB数値で200と255と言っても実はその明るさは大違いであることがわかると思う。
 |
だから、この手の処理を行う際には、まずは指数変換してから処理を行い、そしてその後対数変換してやらなければならないわけだ。もちろん、今回のデジカメ画像をぼかす場合にも、RGB画像の数値をまずは指数変換した後、「ボケ」演算を行って、その演算結果を対数変換でRGB画像の数値に戻してやらなければならないのである。といっても、別に難しい話ではなくて画像を扱う装置だとごく当り前の話だ。
そう、「ボケ」演算のhirax.net風レシピはたったこれだけ〜というわけで、早速このレシピに従ってhirax.net風デジカメ「ボケ」フィルターをかけてみたのが下の画像である。キレイな「ボケ」画像ができあがっていることが判ると思う。
 |
ところで、デジカメ画像のRGB画像の数値を指数変換したものに「ボケ」演算を行ったわけだけれど、もしRGB画像の数値そのものに対して「ボケ」演算を行ったら、どんな結果になるだろうか?つまり、「データ上の数値をそのまま拡散させる」やり方をしたら、どうなるのだろうか?そこで、試しにRGB画像の数値そのものに対して「ボケ」演算を行ってみるとこんな結果になる。
 |
何だかボンヤリとにじんだだけの「キレイじゃない」写真になってしまっている。それは、当り前である。本来2倍明るいものはX^2倍明るいわけで、すごく光の量は2倍どころでなく多いわけだ。それが広がる量を仮にRGB数値そのまま2倍として扱ってしまうと、その光の部分は薄暗くなってしまう。コントラストのはっきりしない、ぼんやりとした写真になってしまうわけだ。ちゃんと、X^2倍のデータとして扱ってやらなければならないわけである。
試しに、指数処理したものと線形処理をしたものとを並べてみるとその画像の違いがよくわかるだろう。
キレイなボケ画像(指数処理)  | キレイじゃないボケ画像(線形処理)  |
さて、今回はデジカメ画像の「ボケ」フィルターのhirax.net風レシピを確認してみた。次回(と言ってもいつになるか…)以降に、このレシピに従って実際にソフトを作成していこうと思う。
ところで、「文学論」の中で漱石は「ボケ」は焦点的印象又は観念に付随する情緒を意味する、と言っている。それは、言い換えれば「何かの出来事をきっかけとして感じた怒り・悲しみ・喜びなどの感情がボケである」ということだ。そして、さらに言えば、写真で背景をぼかすということは、つまり「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて包み込む」ということなのである。
だから、何かを撮影する時に対象物の背景をぼかすということは、「背景にある出来事が生みだした怒り・悲しみ・喜びを広く混ぜて対象物を包み込んで、そして対象物を浮き上がらせる」ということなのかなぁ、とぼんやりと考えてみたりする。そんな写真は対象物を写しこんでいるのと同時に、それを包みこむ背景も写しこんでいるンだろうなぁ、と考えてみたりする。

2001-10-12[n年前へ]
2001-12-17[n年前へ]
■モンテカルロでビンゴ大会 
「幹事」のための確率講座
先日、会社の後輩が結婚したので、その結婚式の二次会が新宿で開かれた。会場は、花園神社近くにあるこじんまりとした地下のバーで、多分4〜50人くらいが普通に座ると一杯になる程の広さの店だろう。
そんな広さの店だったのだけれど、主賓のカップルの人徳だろうか、100人弱くらいの人達がその狭い店中に溢れていた。私達(『会社の先輩』と呼ばれる人達)はその一角に陣をとり、ビールを飲みながらカメラ談義などをしていた。EOS-1Digitalや50mmF1.0というレンズを前にして、私の手元にあるSpyzは段違いに情けなく、田代まさしの事件もあったせいで、恥ずかしさすら感じさせるほどだった。
そして、その二次会は四時少し前に始まったのだが、ほどなくビールとワインが進んだ四時半頃にはお決まりのビンゴ大会が始まり、私達もシートを片手に司会者の進行に耳を傾けた。
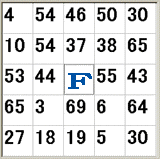 説明も要らないだろうけど、読み上げられた数がシート上にあれば、 穴を開けて、穴が一直線に並べばビンゴだ |
(私を知らない人からは)クールと言われる私でも、何故かビンゴのシートを手にするとドキドキしてしまう。景品がどーしてもどーしても欲しいー、というわけではないのだけれど、やっぱりビンゴのシート片手にドキドキしてしまう。そんなドキドキは私だけではなくて、私の周りもみんなビンゴのシートを手にドキドキしているし、人間でなくてロボコップのようだと評された(評したのはワタシだが)こともある人でさえも、ビンゴのシートを手に司会者の声に耳を澄ませているのだから、きっとそれはみんな同じなのだ。
そして、そんな中、司会者は次々と数字を読み上げていった。が、何回新たな数が読み上げられても私の手元のシートはなかなか穴が増えていかないのである。クジ運が良いとは言えない私のシートがビンゴになかなか近づかないのはいつものことなのだけれど、ワタシの周囲の人もまた同じように全然穴が増えていかないのである。そして、それどころか実は会場全体の人がそうだったのである。全然「リーチ」と声を上げる人もいなくて、狭い会場で100人弱もの人がいるにも関わらず、この遅々たる進行状況はかなり異常なのではないか、と感じてしまうほどなのだ。
で、そのゲームの最中に手元のビンゴのシートを眺めながら私は考えた。なんで、こんなに時間がかかるのだろう?私だけでなく、ここに集う全ての人は不運の持ち主なのだろうか?不運の持ち主が100人集まるとは、これは一体何事だ?不運の会か?と、結婚式の二次会にはとても相応しくない想像さえしていた。
で、そんな相応しくない想像をしながらそのシートを眺めていると、ふと気づいたのである。「ん?99?えっ?きゅーじゅきゅうー?」 この不安な気持ちは何だろう?手元のシートは5x5で高々25個の数字しかないのに、書いてある数は99までもある。ということは、呼び上げられる数字はきっと01から99までの100個。ということは、呼び上げられる数字に対して、手元のシートの「数字」の数は1/4程しかない。それでは、そもそもシート上になかなか穴が開いていかないのではないだろうか?そのペースで一体何回数字を読み上げれば、シート上で穴が一直線に並ぶのだろう?そして、あの何個もある景品達は一体何時になれば全部売れていくのだろう?う〜ん、ビールが回った頭では全然判らないぞー。いや、きっとシラフでも判らないぞー、そして、貸切の時間を考えるときっと司会者もドキドキしてるぞーと思ったのである。
結局、最初にビンゴになった人が出たのが、ビンゴを始めてから20分以上過ぎてからだったと思う。そして、10個ほどの景品が配り終えられたのはビンゴが始まって一時間程した頃だった。つまりは、二次会がお開きになるくらいの時間だった。司会者はかなりヒヤヒヤしていたようだった。
そして、帰りの電車の中で私は考えた。もしかしたら、ビンゴ大会を開く幹事には、確率統計の知識が必要とされるのではないか、と。何人の人達が会場にいて、景品は何個あって、ビンゴのシートには1から何までの数が書かれているから、一分に一個の数字というペースで読み上げていけば、ビンゴ大会にかかる時間は何分だ、と概算できるくらいでないともしかしたらマズイのかもしれない、と思ったのである。少なくともヒヤヒヤしないためには、そんな概算をしておくのも良いかもしれない、と思ったわけだ。
で、そんな司会者・幹事のために、今回試しにビンゴの確率論を計算してみることにした。といっても、私は確率・統計がどうにも苦手なので、モンテカルロシミュレーション(別名下手な鉄砲も数打ちゃ当たる法)である。つまりは、何回もサイコロを振ってシミュレーションしてみただけの話である。PCの中で繰り返し、ビンゴ大会を開催してみただけなのである。ビンゴというギャンブルの確率を計算するのだから、それはもうモナコ王国誇るモンテカルロ・シミュレーション以外ないと思うのである。
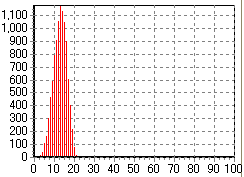
そんなわけで、下に示すのが「何回目でビンゴになるか一万回試行したときのモンテカルロシミュレーションを行ってみた結果」である。実際にビンゴ大会を一万回したらものスゴイ時間がかかるが、PCの中だったら一瞬ですむのが素晴らしいところである。ちなみに、ビンゴのシートの条件は、シートに書かれている数字が
- 01〜24
- 01〜49
- 01〜74
- 01〜99
 |  |
 | 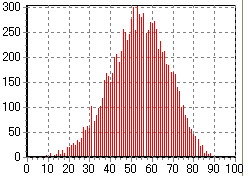 |
これを見ると、例えば、シートに書かれている数字が01〜24までの範囲の場合は、12回目位で半数の人がすでにビンゴになっていることが判る。一分に一個の数字というペースで読み上げていけば、5分過ぎには半数が終了している、というペースである。かなり速いペースである。
それに対して、シートに書かれている数字が01〜49までの範囲の場合ともなると、25回目位でやっと半数である。とはいえ、一分に一個の数字というペースでも、12,3分で半数がビンゴだから、これもやはりかなり速い進行だ。
ところが、さすがにシートに書かれている数字が01〜99までの範囲の場合ともなると、半数がビンゴになるのが、60回目位なのである。先程の数字を読み上げるペースであれば、時間にして30分である。景品の授与の時間などを考えると、かなり時間がかかってしまいそうだ。きっと4,50分ほどはかかることだろう。実際、先日のビンゴ大会はその程度の時間がかかっていたわけである。
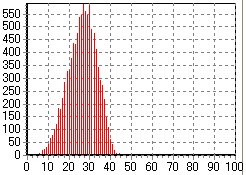
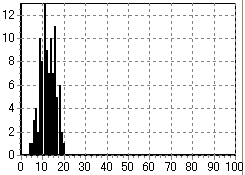
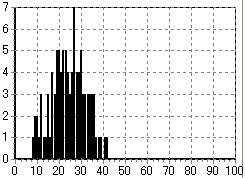
そこで、試しに先日のビンゴ大会と同じ人数でモンテカルロ・シミュレーションをしてみた結果が下である。会場に100人の人がいた場合のビンゴになる人の回数(時間)に対する割合である。
 |  |
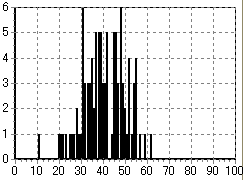 | 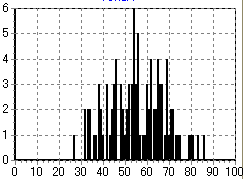 |
この結果だと、会場に100人の人がいた場合、最初のビンゴになる人は
- シートに書かれている数字が01〜24までの範囲の場合 → 4回目
- シートに書かれている数字が01〜49までの範囲の場合 → 8回目
- シートに書かれている数字が01〜74までの範囲の場合 → 10回目
- シートに書かれている数字が01〜99までの範囲の場合 → 27回目
というわけで、これからの忘年会・パーティーシーズンに向けて、「幹事」は電卓を叩いて会費の計算をするだけではなくて、確率・統計の知識もあると便利かもしれない、モンテカルロでビンゴ大会の予行練習をしてみるのも良いかもしれない、と思ったのである。とはいえ、そんな確率統計を計算し尽くした「幹事」もちょっとイヤかも、とビールが回った頭で想像したりしたのだった。
2001-12-27[n年前へ]
2002-02-11[n年前へ]
■めがねっこ大好き。 
めがねを外すと美人になるは本当か!?
理系=めがねっこ大好き? 「どんな時に自分を理系だと思う?」と文系人間に聞かれた。私は「うむむ…」と答えに詰まってしまった。そんな私に、その文系人間はまるで勝ち誇ったような表情で「じゃぁ、理系と文系はどう違うと思う?」と畳みかけるように聞いてきた。この手の数限りなくある、「理系と文系」「男と女」はどう違う?という問いには立ち入ってはいけない、というのが私の家の代々の家訓なのであるが、ここで黙りこんでいては「勝ち負け」でいうところの「負け」だと思ったのか、理系の誇りを守るべく、私の口がいきなりしゃべり出した。
例えば、建築で言えば、鉄骨建築が理系で、プレハブ住宅が文系なのである。体で言えば、皮膚の感覚を大事にするのが文系で、骨から組み立てていくのが理系なのである。つまり理系は骨があるのである。そして、詩で言えば、散文詩は文系で定型詩が理系なのである。つまり、理系は型にこだわる部分があるのである。と、スキーのモーグル競技でコントロールを失い、コースアウトしてしまう選手のように私の口は暴走を続け、理系=めがねっこ大好き、という辺りではもう「勝ち負け」でいうところの「負け犬」であるようにしか思われず、理系の誇りを守るどころか、理系を単に汚しただけに終わってしまった。そこで、悔しさのあまり、今回は「めがねっこ」に対し理系的なアプローチで近づいてみることにした。そして、私が汚してしまった理系の汚名をすすぎたいと思うのである。だから、例えば理系は女子高生の制服が大好きなのである。色々ある女子高生をセーラー服(あるいはブレザー)という記号で記号・集合論的に取り扱うことを可能にし、その記号を言葉にし、ついにはその制服を見るだけで萌えることができるのである。それが理系なのである。
つまりは、「このアイドルがなんとなく好き」というのが曖昧模糊としたものが文系であるならば、「このアイドルがめがねっこだから好き」という確固とした意志それすなわち理系なのである。理系=めがねっこ大好きなのである。
「めがねを外すと美人になる」は本当か!?
よく、少女マンガなどで、「ヒロインが眼鏡をとると美人になった」というストーリーをみかける。今はどうだか知らないが、少なくとも昔はよくそんなストーリーを見かけた。あれは果たして本当だろうか。そして、それが本当であるならばそれは一体どんな物理現象なのだろうか?そして、ヒロインが眼鏡をとると美人になった」というストーリーと「めがねっこ大好き」というそ相反する二つの事象はどんな原因に基づいているのであろうか?それを理系的なアプローチで明らかにしてみたいと思う。
めがねはもちろん視力が悪い場合に、その矯正を行うための道具である。近視の人であれば矯正のために凹レンズをかけるし、逆に遠視の人は矯正のためには凸レンズをかける。凸レンズと言えば、虫眼鏡と同じで、何かの近くにレンズを持っていけばそれが拡大されて見える。また、逆に凹レンズであれば、対象物が小さく見える。
 |
だから、近視の人が凹レンズである眼鏡をかけた場合には、その人の目が他の人からは小さく見えてしまうのである。実世界でも、少女マンガの世界でも大きな瞳は美少女の象徴であるが、近視の人が眼鏡をかけると、大きな瞳を持つ美少女でもちっこい瞳になってしまうのである。
試しに、仲間由紀恵に凹レンズの眼鏡をかけさせた場合の、シミュレーションを行ってみたのが下の結果である。左のめがねをかけた「近視の」仲間由紀恵は確かにキレイではあるけれど、右の仲間由紀恵の方が、美少女という魔性の魅力という点で遙かに勝っていることが判るだろう。
 |  |
そう、近視の人の場合には、「めがねを外すと美人になる」は物理的に本当なのである。近視の人の割合は国によって大きく違うらしいが、少なくとも現代の日本では近視の人の割合は圧倒的に多い。ほとんどの人が近視である、といっても良いくらいである。ということは、そんな日本では「めがねを外すと美人になる」はかなりな確率で事実である、と言えるわけだ。
それでは、「めがねを外すと美人になる」ということと相反するとしか思えない「めがねっこ大好き」現象をどう説明したら良いだろうか?一つは、遠視の場合先の近視の場合と逆のことが起きる、ということである。すなわち、遠視の人の場合には、眼鏡をかけると瞳が大きく見えるのである。すなわち、眼鏡をかければ、美少女の象徴たる大きな瞳が手に入るのである。
下の「遠視の」仲間由紀恵の場合の眼鏡シミュレーションを見てみると、めがねをかけたことでずいぶんと美少女度がアップしていることが判ることと思う。まさに、その瞳には魔性の魅力が宿っているとしか思えないほどなのである。
 |  |
ということは、「眼鏡を外すと美人になる」は本当。ただし、近視の人の場合は、ということなのだ。そして、もし遠視の人であれば、「眼鏡をかけると美人になる」が本当なのである。
とはいえ、日本人では遠視の人は少ないわけで、それではめがねっこを増やす原因たる「眼鏡をかけると美人になる」が少なくなってしまう。そこで、他の原因を考えてみると、例えば近視の人が裸眼の時には瞳の口径を小さくすることで、被写界深度を深くする、すなわちハッキリとものを見ようとして、目を細めがちであること、すなわち小さな瞳になりがちであること、なども原因の一つとして考えられるだろう。
そしてまた、実は近視の程度が低い場合には、「めがねっこ大好き」現象を支えるもう一つの事実がある。レンズの度数がきつくなくて、他の人から見た瞳の拡大縮小が行われないような場合にも、眼鏡をかけると実は心理的に瞳の大きさが変わって見えるのである。
下の「目が小さい」仲間由紀恵は左右で目の物理的な大きさは完全に同じである。が、心理的には結構違って見える。眼鏡をかけた仲間由紀恵の方が目が大きく見えることが判ると思う。「目が小さい」場合、めがねをかけると瞳が大きく見えるのである。
「目が小さい」仲間由紀恵  | 「目が小さい」仲間由紀恵  |
日本人は目が小さい人が多いから、このような眼鏡をかけると心理的に瞳が大きく見える影響は無視できないに違いない。
ところが、目がもともと大きい場合には、この現象はそれほど大きく現れるわけではない。もともと瞳が大きいがために、眼鏡をかけたからといって割合的にそれほど瞳が大きく強調されたりはしないのである。その例を下に示す。下の二枚は目の物理的な大きさは完全に同じなのであるが、心理的に受ける瞳の大きさ=美少女度の違いは上の例ほどではないことが判るだろう。
「目が大きい」仲間由紀恵  | 「目が大きい」仲間由紀恵  |
ということで、
- 瞳が多きい近視の人の場合、眼鏡を外すと美少女になる
- 目が小さかったり、遠視だったりする人の場合、「めがねっこ」=美少女になれる
ところで、理系と文系…
さて、理系的「めがねっこ大好き論」も良いのだが、話をそもそもの「どんな時に自分を理系だと思う?」という問いに戻ろう。
よく私が見かけるパズルは大抵が論理的なパズルだ。論理的=理系ではないから、それを理系パズルと呼ぶのはいけないと思うが、あえてそれを理系パズルと呼んでみる。間違っているのを承知で、あえてここではそう呼んでみる。
そんな理系のパズルでもやっぱり色々あるだろう。大抵のそんなパズルの答えは答えがただ一つに限られるものだろうが、時にはその答えが無限にあるものもあるかもしれない、そして答えが一個もないパズルだってあるかもしれない。そしてまた、「答えを見つけられないこと」を証明できるようなパズルだってあるだろう。だけど、いずれにせよ、そのパズルを解く過程で現れようとする「割り切れない何か」は「それが割り切れる軸」を駆使することで、巧妙に消し去っていくことができる。だから、とてもそれは結構気持ちが良い作業だ。少なくとも、私にはそうだ。あるいは、答を判定するものが、自分ではない論理なり自然現象に任せられているから楽なのかもしれない。
だけど、もしそんな論理的なパズルとは違う非論理的なパズル、ここではあえて文系のパズルと呼ぶようなものがあったとしたら、その答えは「割り切れない何かを拾い集めたようなもの」であるような気もする。そして、その解く過程はもしかしたら割り切れない感情や雰囲気を拾い集めて、割り切れないままに何とか答えを投げ出しいく作業であったりするのかもしれない。それに、そこでは答を判定する何かなんかそもそも存在しないか、あるいはその判定する何かが人であるのかもしれない。
私には、そんな「割り切れないままに何とか答えを出していく作業」はちょっと辛いなぁと思う。やっぱり、私は理系パズルの方がずっと楽で気持ちが良い。だから、今度「どんな時に自分を理系だと思う?」と聞かれたら、そんなことを上手く言えたらいいな、と思う。いつも、思い浮かべたことを伝え続けたいな、と思う。