1998-01-08[n年前へ]
■Photohoの乱数プラグインを作成する 
「2項分布のムラについて考える」の関連して、Photoshopの乱数プラグインを作成したのでメモしておく。 PhotShopはとても便利なソフトである。画像を取り扱うにはトップクラスと言っても良い。あえて、難を挙げるならば8Bit階調が基本という所である。もちろん、12bit階調なども扱えるのは知っているが、基本機能とは言えないと思う。
しかし、PhotoShopで凝ったことをしようとすると、Pluginを作らざるを得ない。PhotoShopでPluginをつくるには2つのやり方がある。それは、
- Adobe提供のPlugin SftwareDevelopmentKitを使ってPluginを作る。
- FilterFactoryを使ってPluginを作成する。
今回はランダムノイズをつくるためのプラグイン作成が目的である。その程度であれば、FilterFactoryを使うのが簡単で良い。
 | まずは、FilterFactoryを使う。 |
まずは、Redチャンネルにのみ乱数を与えるものをつくる。以下がそのパラメータである。
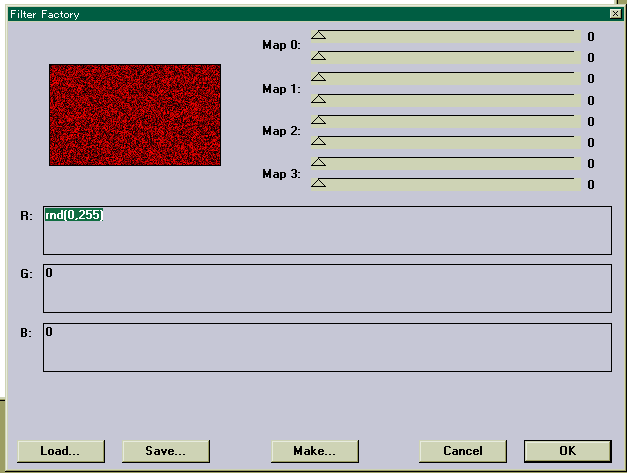 | たった、これだけである。 Redに乱数を与え、Green,Blueのチャンネルには0を与える。 |

もうひとつ、各色に乱数を与えるプラグインのサンプル画像はこのようになる。

さて、試しに使ってみる。1000x1000ドットのランダムノイズ画像を作成してみる。その画像はここに載せるには大きすぎる。そのため、その一部を左下に示す。その画像に対して各領域10x10の100ドットで平均し、100x100に変換した画像を右に示す。詳しくは「2項分布を考える」を見て欲しいが、100ドットで平均したくらいではフラットにはならない。それどころか、有限のいくら広い範囲で平均しても正確にはフラットにはならない。もし、フラットになるのであれば、それはランダムな2項分布ではない。もちろん、PhotoShopの丸め誤差とかの話は別にしておく。また、「2項分布を考える」の際は1次元の1成分データであったが、今回は2次元3成分データである。そのため、人間にはよりフラットに見えにくい。相対的な色差に対しては人間の目は敏感だからである。
 |  |
今回の例も「2項分布の特性:どんなに広い領域であっても、領域中の平均が一定でない」の当然の結果である。仮に、ある広い領域中の平均が一定であるような確率過程を用いればこのようなことは生じない。もしも、そのような確率過程に基づくものがあったら、部分部分はランダムに見えても、広い領域ではフラットに見えるのである。
1998-11-22[n年前へ]
■OHPによるモアレと光の干渉の相似について考える。 
ヒラックス・ディザの提案
「位相保存ディザマトリックス」
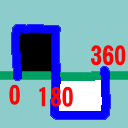
まず初めに、4 x 1ドットからなる基本マトリックスを考える。その各ドットは白か黒の値を持つ。例えば、このような感じである。 |
この「黒、黒、白、白」というパターンを次の図と見比べる。
 |
 |
「モアレのデバイス依存について考える。」で行ったようにこのようなパターンをOHPで打ち出し、重ね合わせてみる。例えば、位相0と位相180のものを重ね合わせたらどうなるだろうか。4x1ドットのマトリックスの全てが黒になる。すなわち、真っ黒になるのがわかるだろう。それでは、位相0と位相90のものではどうだろうか。4x1ドットのマトリックスの内、3ドットが黒、1ドットが白である。位相が同じものどうしを重ね合わせると、元と同じく、2ドットが黒、2ドットが白である。
ということは、「位相が同じ物どうしであれば、元の明るさを保持する」、「位相が逆であれば真っ黒になる」、「位相が少しずれているのあれば、明るさはその分少し暗くなる」という性質があることがわかる。光の干渉の場合とほとんど同じ性質を持っているのがわかると思う。違うのは、同じ位相のものどうしが重ね合わさった時に、重ね合わせた分明るさが2倍になるか、そうでなくてそのままなのかという違いだけである。
つまり、この4x1ドットのマトリックスは「きちんと演算が成立する位相情報が記録されている」ということになる。そして、位相が異なるものを重ね合わせた時の位相情報の保存までも考えてやるならば、先ほどの例1は次のように位相の定義を変えてやるほうがいいと思う。
 |
この例2では位相の数字は各矩形波の中心位置を現すことにしている。それでは、この定義を用いて、位相90,180のものを足しあわせたらどうなるだろうか。下に示すのがその結果である。
 |
位相90と位相180のものを足しあわせると、波形はブロードになり、中心すなわち位相135のものができているのがわかる。また、明るさはこれまでが、2/4だったものが1/4であることになり、強度も弱まっているのが表現されている。
つまり、このようなマトリックスによる表現は波の持つ位相と強度と波形を表現し、演算も成り立っていることがわかる。それでは、例2の基本マトリックスが縦方向に繰り返されている画像(1(基本マトリックス)x8ピクセル)を考える。こんな感じである。
  |
これは下方向から進行している矩形波の様子そのままである。なお、この図でも基本となるマトリックスは4x1ドットであるから、この例では要素としては1x8ピクセルを示しているのである。どの要素も振幅(強度)自体は同じである。平均の明るさは同じである、と言い換えても良い。また、波形自体も同じである。しかし、位相が異なっている。波の進行そのままである。
さらに強度情報を加える
このような白、黒のみの2値表現(といってもこの表現にはモアレが欠かせず、そのためには2値表現がふさわしい)では、波の位相、波形、強度を独立に変化させることはできない。例えば、波の波形を変えると強度も変わってしまう。それを独立にしてやろうと思ったら、階調を増やしてやれば良い。しかし、2値表現のままという制限付きであるから、面積階調を使うことになる。これまで4x1ドットのマトリックスで表現していたものを、例えば、4x4ドットのマトリックスにしてやればよい。以下にその例を示す。例Aの強度が例Bの1/4であることがわかるだろう。 |
 |
このような「位相、波形、強度情報を保存し、演算も成立する」マトリックス表現を仮に「HiraxDither(ヒラックス・ディザ)」と呼ぼう。先の「モアレのデバイス依存について考える。」で使ったスペックルパターンの例はこのヒラックス・ディザの簡易なもの(2x1基本マトリックスのもの)を使っていた。
また、「モアレのデバイス依存について考える。」で使った同心円状の画像のモアレのパターンは実はヒラックスパターンの特殊な例(1x1基本マトリックスのもの)を用いていたのである。そこでは、単に位相情報しか記憶されていない。この場合には、白、黒が位相情報を現していたのである。だから、黒、黒どうしの所(すなわち、位相が同じ所)では平均の明るさは変化せず、黒、白が重なった部分(すなわち、位相が反対である所)でのみ打ち消し合い、暗くなっていたわけである。波形も、強度情報もこの場合には記録されていない。
「ヒラックス・ディザ」とホログラフィーの相似点
このようなヒラックス・ディザの「ディザ・パターン内部、すなわち、微視的には位相情報や振幅情報を記録し、巨視的に見ると強度分布のみが認識される。また、相互の演算(干渉)によって違う画像を再生することができる。」という特徴は実によくホログラフィーと似ていることがわかる。 また、もう少し深く考えると、もっと他の分野とも繋がるかもしれない。いずれ、また考えてみたい。
1999-09-08[n年前へ]
■続ACIIアートの秘密 
階調変換 その1
さて、今回は
の続きである。今回はASCIIアートの階調変換に関する話である。原画像からASCII文字画像に変換するときにどう変換するか、という話の第一話である。 まずは、白から黒までの256階調の基準チャートとASCII文字によるチャートを示してみよう。
両者ともかなり縮小表示している。従って、ASCII文字チャートの方は文字がつぶれて滑らかに見えている。一見すると、ASCII文字チャートの方は白地に黒い文字を印字しているため、完全に黒いようなものは出力できない。そのため、全体的に白く見える。
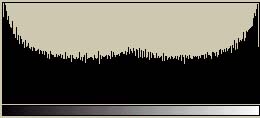
これらの2つの画像のヒストグラムを示してみよう。ばらつきが多少あるが、256階調の基準チャート(上)では256階調にわたって存在している。しかし、ASCII文字チャート(下)では(ざっと見た限りでは)35階調程度しか存在していない(これは使用するフォントによって異なる)。もともと、ASCII文字は数多くあるわけではないし、平均濃度が等しい文字も存在するので、この程度になってしまうのはしょうがない。また、最も黒い領域でも、256階調の基準チャート(上)の半分程度の濃度しかない(これも使用するフォントによって異なる)。
ところどころに「使用するフォントによって異なる」という注釈を入れいるがこれが前回作成したimage2asciiの特徴である。指定のフォントを用いて画像出力を行った結果を用いてガンマテーブルを再構成するのである。逆にいえば、その指定のフォントを用いない場合には意図した画像は得られないわけである。「DeviceDepend」な技術というわけである。
 |
 |
そもそも、オリジナルの画像から、この程度の階調しかないASCII文字画像へどのように変換したら良いだろうか? 先に基準チャート(上)とASCII文字チャートの例を示したが、そもそもそのASCII文字チャートはどのようにして変換するのだろうか?
まず思いつくのはオリジナル画像の濃度に一番近い濃度の出力を行う方法である。それを濃度精度重視の変換と呼ぼう。そして、もうひとつは、オリジナル画像の中での相対濃度を基準とする変換である。すなわち、オリジナルの最大濃度をASCII文字出力による最大画像に合わせ、オリジナルの最小濃度をASCII文字出力による最小画像に合わせ、あとは単に線形に変換する方法である。こちらを(まずは単純な)階調性重視の変換と呼ぼう。その変換の構造を以下に示してみる。
 |  |
濃度精度重視の変換(左)では、ある濃度以上になると全て同じ濃度で示されてしまう。階調性重視の変換(右)ではそんなことは生じない。しかし、オリジナルの画像と変換後の画像の濃度はかなり異なってしまう。これら2つのやり方によるASCII文字チャートをそれぞれ示してみる。
濃度精度重視によるASCII文字チャートと階調性重視によるASCII文字チャート(下)のどちらが自然だろうか?濃度精度重視によるASCII文字チャートは階調の中程までは基準チャート(上)と非常に近い濃度を保っている。そのかわり、それ以降の濃度が高い部分はまったく階調性を失っている。少なくともこの基準チャート(上)のように256階調にわたり均等に濃度が存在するような画像を扱うのであれば、階調性重視によるASCII文字チャート(下)の方が自然だろう。というわけで、前回作成したimage2asciiは階調性重視による変換を用いている。
さて、今回は256階調全てにわたって滑らかな基準チャートを用いて考えてみた。しかし、実際の写真はそんなものではない。色々な濃度が均等に現れるわけではないし、そもそも狭い濃度領域しかない画像の場合もあるそういった場合には、数多くの問題が生じる。また、単に(単純な)階調性重視によるASCII文字チャート(下)が優れているわけでもなくなる。場合によって何が優れているかは異なるのだ。一般的な画像において、一体どんな問題が生じるのか、ということを次回に考えてみることにする。そして、新たに2種類の変換方法を加えてバージョンアップしたimage2asciiの登場するわけである。
今回は、その3つの変換方法の違いにより出力画像にどのような違いが生じるかを示すだけにしておく。先入観が無い状態で、優劣を判断してみると良いと思う。次の例は人物写真である。まずは、オリジナルの写真である。
 |
以下にimage2asciiを用いて変換したものを示す。
 |  |  |
これらの違いがどのようなものであるかを次回に考える。
1999-09-17[n年前へ]
■モアレ、デバイス、2項分布の三題話 
淡色インクの副作用
今回は、9ヶ月間も寝かせた伏線にまつわる話である。いや、別に寝かせるつもりは無かったのだが、いつのまにかそんなに時間が経ってしまった。
以前、
という話があったが、その2つを結びつけるミッシングリンクについて考えてみたいと思う。「2項分布のムラについて考える(1999.01.08)」の最後に「今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、続く...」と書いた。「その続き」というわけである。始めに「2項分布のムラについて考える(1999.01.08)」の要点をまとめると以下のようになる。それは、
- ランダムと呼ばれるものの内で代表的な2項分布においては、当然のごとく「ある領域での平均値はばらつく」。
- そして、そのばらつきは直感的に考える程度よりももっとばらつく。
- 例えば、2値画像で考えるならば、2048dpi程度の解像度でランダムなデータを並べた場合には、人間の目はざらつきを感じてしまう。
そして、「モアレはデバイスに依存するか?(1998.11.20)」での要点は
- モアレにはデバイス依存性がある
- 線形な重ね合わせが成り立たない場合にはモアレが発生する。
最近のインクジェットプリンターはCMYKの4色インクだけでなく、淡色インクも使うものもある。淡色のインクを使うことで階調豊かな画像を印字できるわけだ。4色インクだけではディザなどを使って、解像度を下げて階調を出さなければならないわけであるが、それが不要になるわけだ。
解像度を下げないですむわけであるから、ディザのざらつきを感じないですむわけだ。しかし、淡色のインクを使った場合の効果というのはそれだけではないように思われる。HP(ヒューレッドパッカード)などのWEBのプリンター紹介を読んでいると、「淡色のインクを重ねて濃度を出す」というような記述を目にする。これは「少なくとも淡色インクでは線形性(あるいはそれに近い関係)が成り立つ」ということだ。
インクジェットプリンターの解像度を上げたときに、インク滴が意図しないところへずれてしまうことはきっとあるだろう。その際に他のインク滴と重なったらどうなるだろうか?意図しなくても他のインク滴との重ね合わせは発生してしまうだろう。
重ね合わせが成り立たない、非線型なインクではモアレが発生する。言いかえれば、意図しない濃度のばらつき・ざらつきが発生してしまう。「2項分布のムラについて考える(1999.01.08)」で考えたようにランダムに重ね合わさるから広い領域では一定だろうというのは予想外に成り立たないのである。でたらめというのは私の予想外に大きく効いてくるのである。
しかし、重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しないことになる。参考までにインクジェットの印字画像の拡大写真を示してみる。
 |  |
「重ね合わせに線形性が成り立つ淡色のインクではモアレが発生しない。すなわち、いくらランダムにインク滴の重ね合わせが生じてしまったとしても、意図した通りの濃度をだすことができ、ばらつき・ざらつきは発生しない」と、書いただけでは意図するところが伝わらないと思うので、「モアレはデバイスに依存するか?(1998.11.20)」で使った画像を用いて考えてみる。この画像は重ね合わせがある幾何学模様で生じているが、この現象がランダムに起こっているものとして読み替えて欲しい。
 |  |  |
下は、淡色のインクで重ね合わせ(インク滴の意図しない重なり)が生じた場合である。
 |  |  |
なんの模様も生じていなく、意図した通りの画像出力ができているのがわかると思う。
ということで、今回の話(というか前の2回の話)の繋がりは、
淡色のインクを用いたインクジェットプリンターでは、意図しないインク滴の重ね合わせが生じてしまっても、濃度変化が生じにくく、意図しないインク滴の重ね合わせがでたらめに発生してしまったとしても、画像にはあらわれない可能性があるということである。
うーん、マニアックな内容だ。「身近な疑問を調べる」という看板に偽り有り、である。しかも単なる推論だ。
しかし、もしもインクジェットプリンターを買う人がいるならば、淡色のインクを使っているものを購入するといいかもしれない、ということがわかっただけでも良しとしておこう。
1999-10-15[n年前へ]
■続々ACIIアートの秘密 
階調変換 その2
前々回の
の時にASCIIアートに関する情報を探した- 清竹's テキスト絵 HPリンク集 (http://www2.nkansai.ne.jp/users/kiyo/ )
「限られた出力階調を有効に利用するため、画像の濃度ヒストグラムの補正を行ないます。1パス目で、濃度ヒストグラムをカウントし、そこからヒストグラムが平坦になるような濃度変換関数を生成します。(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」とある。Q02TEXTはimage2asciiと同様のテキストアート作成プログラムである。前回のの最後で(3).情報量を最大にするモデル というのを導入したが、これがそのエントロピー最大化アルゴリズムに近いものを導入してみたものである。何しろ、この考えを使っていくのは乏しい階調性の出力機器には非常に有効なのだ。今回は、この「エントロピー最大化アルゴリズム」について考えてみたい。
Q02TEXTは「 .:|/(%YVO8D@0#$」の16階調を使用するテキストアート作成プログラムである。それに対して、「ASCIIアートの秘密」で作成したimage2asciiが使用可能な階調数は一定ではない。指定されたフォントを一旦出力してみて、その結果を計測することにより、出力可能な階調数を決定している。したがって、指定したフォントでしか階調の確かさは保証されない。その代わりに、指定されたフォントを使えば割に豊かな階調性を使用できることになる。
また、得られる階調は一般的に滑らかではないので、Q02TEXTが使っているアルゴリズムとは少し違うものを導入している。
通常ASCIIアートは色々な環境で見ることができるのがメリットの一つである。しかし、image2asciiはフォントを限定してしまっている。これは、目的が通常のASCIIアートとは異なるからである。私がimage2asciiを作った目的は、それを仮想的な出力デバイスとしてみたいからである。その出力で生じる様々な問題を調べたり、解決してみたいのである。
さて、前回の最後に示した3種類の画像変換は
- 単純な階調重視モデル
- オリジナルの0を出力画像の最小値に
- オリジナルの255を出力画像の最大値にする
- 拡大した単純な階調重視モデル
- オリジナルの最小値を出力画像の最小値に
- オリジナルの最大値を出力画像の最大値にする
- 情報量を最大にするモデル
- エントロピーを最大にするための階調変換を行う
これら3つの変換方法の違いにより出力画像にどのような違いが生じていたかを、まずはもう一度見てみる。まずは、オリジナル画像である。これは、「私の尊敬する」S大先生である。私は尊敬とともに「ロボコップSさん」あるいは、「ロボSさん」と呼ぶのだ。いや、本当に。
 |
以下にオリジナル画像及びimage2asciiを用いて変換したものを示す。
 |  |  |  |
- (1).単純な階調重視モデルが比較的白い個所では一番オリジナルに忠実な濃度であることはわかるだろう。ただし、黒い部分に関しての表現力は極めて低い。
- (2).階調性を少しだけ改善したものではそれより視認性が改善している。
- (3).視認度の高い画像ではあるが、オリジナルとは濃度などは異なる?
それでは、これらの画像のヒストグラムを調べてみる。先の「(ヒストグラムを平坦にするのは、情報のエントロピーをなるべく保存するためです。)」というのとの関係を調べたいわけである。
 |  |  | 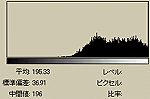 |
ASCII ARTには濃度の表現領域には限度がある。そのため、(1),(2),(3)はいずれも濃度が最大を示す個所でもオリジナルよりかなり濃度が低い。また、(1),(2)はオリジナルとヒストグラムの形状も少しは「似ている」が、(3)においては、かなり異なっているのがわかると思う。(3)はヒストグラムの形状はかなり異なるにも関わらず、視認度は高くなっている。これが、エントロピーを最大化(すなわち情報量を最大化)しているおかげである。ヒストグラムがかなり平坦になっているのがわかるだろう。
というならば、エントロピーの計算もしなければならないだろう。もちろんエントロピーと言えば、
でも登場している。「エントロピーは増大するのみ...」というフレーズで有名なアレである。情報量を示す値だといっても良いだろう。せっかく、「ハードディスク...」の回で計算をしたのだから、今回もその計算を流用してエントロピーを計算してみたい。といっても、無記憶情報源(Zero-memorySource)モデルに基づけば、ヒストグラムが平坦すなわち各濃度の出現確率が等確率に近いほどエントロピーは高いのが当たり前であるが... この前作成したMathematicaのNotebookを流用するために、オリジナルと3つの変換画像を合体させる。そして、そのヒストグラムを見てみよう。このヒストグラムが非常にわかりにくいと思うので、一応説明しておく。あるY軸の値で水平に1ライン抽出して、その部分のヒストグラムを右のグラフに示しているのである。
 | 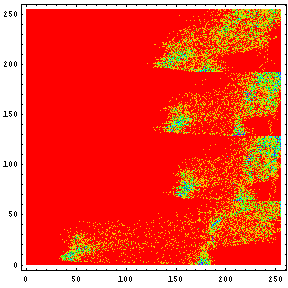 |
例えば、オリジナルの画像では髪の毛がある辺り(Y軸で10から30位)では、ヒストグラムを見ればレベルが50位の黒い所が多いところがわかる。それに対して、変換後の画像では、一番濃度の高い所でも150前後であることがわかるだろう。
それでは、それぞれ、Y軸でスライスしてその断面におけるエントロピーを計算したものを次に示してみる。
 | 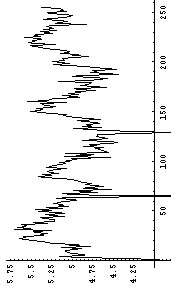 |
本来は、画像全面におけるエントロピーを計算するのが、望ましい。しかし、ここで使っているような、Y軸でスライスしてその断面におけるエントロピーでも、オリジナルの画像が一番エントロピーが高く、(3)の変換画像(つまり一番上)のものが次にエントロピーが高いのがわかると思う。つまり、情報量が高いのである。
エントロピー量とあなたの感じる「視認度」とが相関があるかどうかは非常に興味があるところだ(私にとって)。エントロピーが多くても(すなわち情報量が多くても)オレはちっともいいと思わないよ、とか、おれは断然エントロピー派だね、とか色々な意見があったらぜひ私まで教えてほしい。
「お遊び」に見えるASCIIアートも、調べていくと実は奥が深いのだなぁ、とつくづく思う。といっても、もちろん本WEBはお遊びである。なかなか、奥までは辿りつかない(し、辿りつけない)と思うが、この「ASCIIアートの秘密」シリーズはまだまだ続くのである。