1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。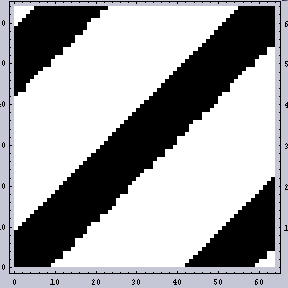 | 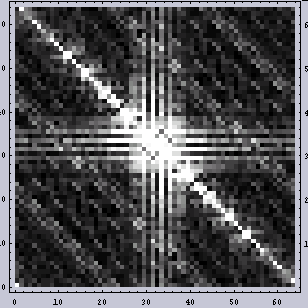 |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる
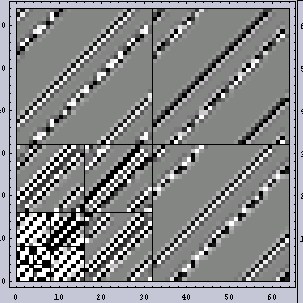
なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 | 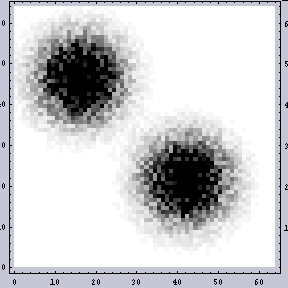 |
 | 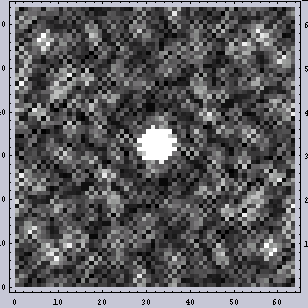 |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
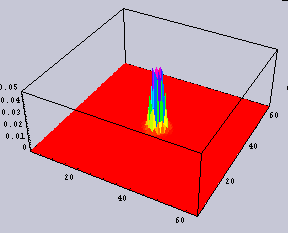 | 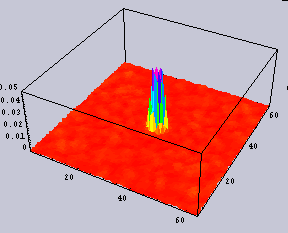 |
 |  |
1999-02-28[n年前へ]
■分数階微分の謎 
線形代数、分数階微分、シュレディンガー方程式の三題話
分数階微分?
InterLabの1999No.5を読んでいると面白い記事があった。いわき明星大学理工学部の榊原教授の「Waveletと数式処理ツール」という記事である。といっても、興味を持ったのはWaveletのことではない。もちろん、Waveletに興味がないわけではない。この榊原教授が講師を務めたWavelet講習にも参加したこともある。しかし、今回興味を惹かれたのはその記事中にあった「分数階微分の解析」である。InterLabの榊原教授の記事を引用すると、-通常微分・積分は整数回実行できるが、分数階微分はこれを分数に一般化したものである。さまざまな物理や工学の現象の記述に使われるようになった-とある。一階微分とか二階微分というものはよく使うが、0.5階微分などというものは使ったことがない。どのようなモノなのかさえよくわからない。
参考:
一体、どんな物理や工学の現象の記述に使われているのか知りたくなったので、infoseekで調べてみる。すると、いわき明星大学の清水・榊原研究室の「粘弾性動モデル」が引っ掛かる。
参考:
衝撃吸収・シリコーンの弾性率などに興味を持っている人には面白いかもしれない。もう少し調べてみると「バナッハ空間バナッハスケールにおける分数階積分作用素」というようなキーワードも引っ掛かる。
そこで、まずは勝手に分数階微分について考えてみた。
分数階微分・積分の勝手な想像図
まずは、イメージを考えるためにグラフを作成してみる。x^2の関数、および、それを微分・積分した関数である。微分は3階まで、積分は2階まで行っている。
 |
このグラフ形式の表示をちょっとだけ変えてみる。
 |
ここまでくると、平面グラフにしてみたくなる。つまり、微分・積分の階数を離散的な整数値でなく、連続的な値としてのイメージに変えたくなる。
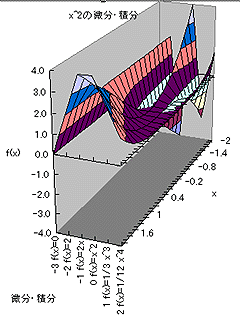 |
これで、微分・積分が整数階でない場合のイメージ(勝手な)ができた。微分・積分が離散的なものではなくスムーズにつながっているものであるというイメージである。図.2から図.3への変化をよく覚えていてほしい。
といっても、これは数学的なイメージのみで物理的なイメージはまだここでは持っていない。位置、速度、加速度などの微分・積分で選られるものに対して同じようなイメージを適用すると、位置なんだけれどちょっと加速度っぽいもの、とか、速度と加速度の「合いの子」みたいなものというような感じだろうか?
さらに、これから先は、f(x)という関数が示す無限個の値を位置ベクトルと考えて、f(x)というのは無限次元空間の一つの点だというイメージを持つことにする。線形代数を考えるならそれが一番わかりやすいだろう。任意の階で微分された関数群が集まって、さらに高次元の空間をなしているというイメージである。
分数階微分を調べる
勝手なイメージはここまでにして、手元にある数学の参考書の中から手がかりを探してみた。すると、大学院入試問題解説 - 理学・工学への数学の応用 - 梶原壌二 現代数学社ISBN4-7687-0190-6
の中に手がかりがあった。あれ、ということは以前にやったはずなのか...そう言えばおぼろげな記憶がちょっと...
その中の言葉を少し引くと、
フーリエ変換は等距離作用素である、関数空間L^2(R)における回転といえる。結局、
となる。そして、古典力学におけるハミルトン関数において、運動量を微分演算子で置き換えれば、量子力学や量子化学のハミルトン演算子が得られ、シュレディンガー方程式などにつながるのである、とある。他の資料を眺めてみると、どうやら量子力学などの分野からの要請に応じてここらへんの微分演算子の分野が発展しているようだ。理論物理などをやった方ならよくご存知のことだろう。例えば、水素原子の基底状態の波動関数へ運動エネルギーの演算子を作用させるというような、基本的な所でも、このフーリエ変換を用いた微分演算が用いられてる。ここで、fは元の関数であり、Fはフーリエ変換
さて、この式自体は非常に簡単である。それにイメージも湧きやすい。
i を掛ける演算、私のイメージでは複素数空間の中で90度回転をする(言い換えれば、位相が90度ずれる)演算、が微分・積分であるというイメージはスムーズに受け入れやすい(それが正しいかどうかは知らないが)。なぜなら、微分が空間の中での回転であるとすると、三角関数の微分・積分に関する性質(例えば、Sinを微分するとCosに、Sinを2階微分すると-Sinになる、すなわち、一回の微分につき位相が90°ずつ回転する(位相がずれる)というような性質)が納得でき、それがフーリエ変換という形で登場してくることがスムーズに受け入れられるのである。また、微分といえばとりあえず三角関数の登場というイメージもある。
もう少しわかりやすく書くと、
- 三角関数では一階微分の結果は90度位相がずれる(回転する)。
- ならば、(例えば)0.5階微分は45度位相をずらせば良い。
- 任意の関数もフーリエ変換により、三角関数に分解される。
- ならば、任意の関数に任意の実数値の微分が成立する。
任意の関数をフーリエ変換し三角関数に分解した時の位相、言い換えれば、周波数領域での位相ずらし、で分数階微分が定義されるということは、物理的実用的に大きな意味を持つ。例えば、電磁波、弾塑性運動などの物理現象の中での位相変化を分数階微分で解けることになる。例えば、複素貯蔵弾性率などについて分数階微分との関係は深そうである。あるいは、媒体中の電磁波の位相などについて適用するのも面白そうである。
分数階微分を使ってみる
よく分からないところも多いが、とりあえず、
という式を使ってみる。まずは、使ってみないとわからない。とりあえず、1次元の関数を作成して、この式を適用してみる。まずは、よく出てくるガウス分布で適用してみる。まずはガウス分布とそれの通常の一階微分の解析解を求める。
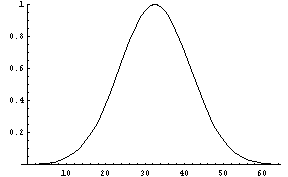 | 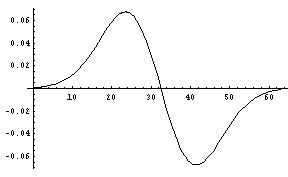 |
それでは、今回の方法による一階微分の結果と、それと解析解との比較を示す。なお、本来無限領域のフーリエ変換を有限の領域で行っているため、端部近くで変なことが生じるのはしかたがないだろう。また、色々な事情により係数の違いは無視して欲しい。
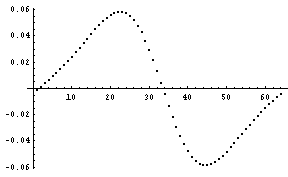 | 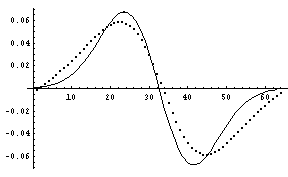 |
ちょっとずれが生じているが、こんなものだろう。しかし、これだけでは今回のフーリエ変換を用いた微分の面白さはでてこないので、0から2の範囲で連続的に分数階微分をしてみる。
 1/10 (=0.1)階微分 |  1/2 (=0.5)階微分 |  7/10 (=0.7)階微分 | 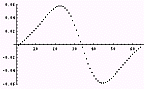 1階微分 |
 13/10 (=1.3)階微分 | 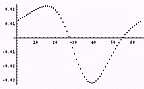 15/10 (=1.5)階微分 | 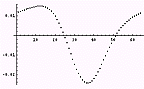 17/10 (=1.7)階微分 |  2階微分 |
モーフィングのようで面白い。
さて、今回は分数階微分を勉強してみる所までで、これの応用は別に行ってみたい。もちろん、言うまでもないと思うが、間違いは多々あると思う。いや、田舎に住んでいるもので資料がないんですよ。
1999-07-08[n年前へ]
■走査線の狭間 
1/60秒の世界を目指せ
あぁ、今回は(今回も)めちゃくちゃマニアックな話である。トップページには「身近な疑問を調べる」、と書いてあるが、他の人にはぜんぜん身近ではないだろう。最近、妙に忙しいので、身近な疑問がおろそかにされているのだ。身近な疑問の解決は結構難しいのである。そのため小難しい話が続くのだ。困ったことだ。
さて、今回やったことを結論から言えば(*)、AVIファイルをフィールド毎に分解してBitmapファイルに落とすプログラムを作ったのだ。「このソフトはとても便利だ」と言ってくれる人がいたならば、感謝感激雨あられだ。とりあえず、私には欠かすのことのできないソフトである。なぜ、このソフトがそんなに便利なのかを、これから手短に(**)語りたい。
* 「結論から言えば」、とか、「要するに」という人は必ず結論を言わなかったり、全く要約されていない話をするのはなぜだろうか?
** 同じく、「手短に」ときたら、必ず話は長くなる。
一般的なTVで使われている信号はNTSCと呼ばれる。1秒あたり約30フレームからなり、1フレームは2フィールドにわけられる。というと、複雑に聞こえるが実はとても単純だ(***)。単に1フレームが奇数フィールドと偶数フィールドに分かれているだけである。フィールドというとわかりにくいので走査線と考えればわかりやすい、と思う。
*** 当然のごとく、単純ではない。
NTSCの信号を時系列で追うとこのような画像の集合になっている。例えば、こういう具合だ。
1フレーム目の奇数フィールド(走査線)
1フレーム目の偶数フィールド(走査線)
2フレーム目の奇数フィールド(走査線)
2フレーム目の偶数フィールド(走査線)
.
.
.
29フレーム目の奇数フィールド(走査線)
29フレーム目の偶数フィールド(走査線)
30フレーム目の奇数フィールド(走査線)
30フレーム目の偶数フィールド(走査線)
30フレームで約1秒であるから、1枚の画像(フレーム)は約1/30秒である。だから、普通のビデオカメラで撮影した画像は1/30分の1秒毎の画像を示しているのである。しかし、もっと高速度撮影したいと思うときがある。ウン百万出せば、1万分の1秒の撮影でも可能な高速度カメラが買えるが、個人ではとても買えない。また、そもそもやりたい用途向けの高速度撮影用のカメラが存在しない場合というのもままあるのだ。そういった場合には、時間軸に対しては1/30秒までの撮影にしか使うことはできない、と思えるだろう。
しかし、NTSCの信号もフィールド毎に分解すれば、1/30秒の半分、すなわち1/60秒毎の画像を示しているのである。たかだか2倍ではあるが、されど2倍である。1/30秒では見えていなくても、1/60秒では見える世界というのもあるのだ。
画像例を用いて説明しよう。左の1/30秒間の画像を奇数フィールドと偶数フィールドに分解したのが右の画像(a),(b)だ。(a),(b)を比べると、黒い矩形が左から右に移動しているのがわかるだろう。今回のソフトウェアはそういった計測には非常に便利なのだ。このソフトウェアを使えば、普通のビデオカメラの性能を2倍にすることができるのだ。スポーツをやる方などは自分のフォームをチェックするのに使うといいだろう(画像解析までしてフォームチェックはしないか、普通...)。これで、フォームチェックはプロ級だ。
| 1/30のままの例 | 1/60のフィールドに分解した例 |
 |  |
 |
1/30と1/60がたかだか2倍でも結構違うという良い例は、1/30秒のシャッタースピードではブレた写真になってしまう人でも、1/60秒なら大丈夫、とか、ゲームを作る際に1/60秒以内に人間からの入力に対して反応を返してやれば、プレーヤーはスムーズに感じるが、1/30秒ではダメだ、とかいう話がある。
というわけで(****)、AVIで記録された動画ファイルを1/60毎の画像に分解するプログラムが今回作成したものである。
 |
奇数フィールドと偶数フィールドを分けることにより2枚の画像に分解し、それぞれの画像内で失われたフィールドを単純補間により復元することができる。奇数フィールドが先頭か、あるいは、偶数フィールドが先頭かは選ぶことができるし(奇数フィールドと偶数フィールドのどちらが先か選べるということでもわかるように、どちらが先であるか必ずしも決まっているわけではないらしい。そこらへんは、各映像機器によって変えなければならない。)、インターレースでなくノンインターレースの場合、つまり、単にAVIファイルの各画像を静止画におとすことだけもできる。
**** 「というわけで」は話を強引に次へつなげるときに使う。
このプログラムを使ったあとはScion ImagePCを使うのがお勧めだ。Macintoshの世界で一般的なNH-imageのWindows版である。今回のプログラムで作成した静止画群をスタック化して使うのがいいと思う。そうそう、Scion ImagePCに読む込むときには静止画を8bit(gray)画像へと前処理しておくことがお勧めだ。
1999-10-07[n年前へ]
■CCDカメラをバラせ! 
モアレは自然のClearText
あまり、「できるかな?」では工作の話題が出ていない。いや、もしかしたら全然出ていないかもしれない。そこで、手元に8mmビデオのジャンクがあったので、こいつをバラしてみることにした。そして、これまで「できるかな?」に登場しているような話に関連していることがないか調べてみるのだ。いや、本当は嘘で計画済みの伏線張りまくりの話である。もしかしたら、勘のいい方はもう話の風向きはもうおわかりかもしれない。
さて、今回分解するカメラはかなり前(といっても数年前)のモデルである。まずは、分解してみよう。
 |  |  |
 |  |  |
 |  |
5.の写真でわかるように、CCD前部にはフィルターが着けてある。(当初はこれを赤外線フィルターだと考えていた。なので、このフィルターを外してやると、画質はとんでもないことになる。しかし、その上で赤外線投光器を装着すれば面白いカメラになりそうである。が、用途を間違えるととんでもないことになるので、今回はやらない。が、いつかやってみようとは思っている。もちろん、私は品行方正がモットーであるので、悪用はするわけがない。もちろんである。)と、書いたがその後、「これは赤外線とは逆のエイリアシング防止用のハイカットフィルタだろう」というご指摘を頂いた。フィルターが青色だったので、単純に赤外線カット用途かと思い込んでいたが、どうやら違うらしい。指摘の文章をそのまま、使わせていただくと「CCDは空間サンプリング素子であり、サンプリング周期(ピクセルのピッチ)よりも短い波長の光が入ると、エイリアシング(折り返しノイズ)を生じて擬似カラー、干渉縞を生じてしまいます。これを避けるためのハイカットフィルタです。」とある。その後、知人から頂いた資料(勉強しなおせ、ということだろう)を読むと、水晶板をだぶらせて2重像にすることにより、細かい解像ができないようにしているローパスフィルターであるようだ。空間周波数のローパスである。今回のCCDでは3層構造になっており、中央の層にのみ色がついている。反省がてら、次回にもう少し調べてみようと思う。
ところで、7.などの拡大画像で周辺部が丸くケラれているのがわかると思う。これは、
と同じく実体顕微鏡の接眼部からデジカメで撮影を行っているからである。デジカメはこういう時に何より重宝する。さて、デジカメと言えば、こちらも同じくCCDを用いているわけである。さて、8.の拡大画像を見ると、このカメラのCCDのカラーフィルターは補色方式(CMYG=シアン、イエロー、マゼンダ、グリーン)であることがわかる。原色タイプでないところを見ると、どうやら感度重視の製品であるようだ。また、この拡大画像などを眺めると、
で調べた液晶のフィルターと同じような構造であることがわかる。よくストライプ模様の服を着ている人をCCDビデオカメラで撮影すると、モアレが発生することがあるが、それはこういったフィルターの色の並びに起因しているわけである。フィルターの周期とストライプの模様が干渉してモアレが生じてしまうのである。 最近のものではソフト的にかなりの処理をしてモアレが出にくいようにしているし、CCDも高解像度化が進んでいるので、なおさら出にくい。私が使用している富士写真フィルムのFinePix700でそのようなモアレを出そうと思ってみたが、なかなか出なかった。むしろ、ピントを正確に合わせることができなかった。それでも、何とか白黒の縦線模様を撮影して、モアレを出してみたのが下の写真である。左がオリジナルで、右がそれに強調処理をかけたものである。
 |  |
モアレが発生しているのがわかると思う。さてさて、こういう白黒ストライプをよく眺めてみれば、
で登場したこの画像を思い出すはずだ。 |  |
そう両者ともまったく同じ斜線である。そもそも、前回作成したパターンは今回への伏線であったのである。白黒の縞模様を撮影しているのであるから、普通は白黒模様しか撮影されない。しかし、モアレが発生している場合というのは、CMYGからなる1画素の中でのさらに細かな位置情報が判るのである。先ほどのCCDの色フィルターの拡大写真のような配置になっていることを知っているのであるから、その配置も考慮の上処理してやれば良いのである。もちろん、白黒の2値からなる画像を撮影しているという前提条件は必要である。その前提条件さえつけてやれば、モアレが生じていることを逆に利用して、高解像処理ができるはずだ。
例えば、
| Green | Magenda |
| Yellow | Cyan |
という画素のGreenだけ出力が大きかったとすると、グレイ画像であるとの前提さえ入れてしまえば、1画素のさらに1/4の領域まで光が当たっている位置を推定できるということになる。もちろん、実際のカメラでも4色の間で演算をしてやり、ある程度の推定はしているだろう。しかし、前提条件を入れてやれば、より高解像度が出せるだろう。
ClearTextの場合は白黒2値の文字パターン、あるいはハーフトーンという前提条件をつけて液晶に出力を行った。今回は、白黒2値の文字パターン、あるいはハーフトーンという前提条件をつけて、CCDからの出力を解釈してやれば良いわけである。CCDカメラにおいては自然が自動的にカラーシフト処理をしてくれるのである。そのカラーシフト処理からオリジナルの姿を再計算してやれば良いわけである。もっとも、これらのことは光学系がきちんとしている場合の話である。
今回考えたような、そういった処理はもうやられていると思う。FinePix700でも撮影モードに
- カラー
- 白黒
 |  |
うーん、白黒のほうがキレイなような気もするが、よく判らない。念の為、強調処理をかけてみる。もしかしたら、違いがわかるかもしれない。
 |  |
うーん、これではますます違いがよくわからない。これは、次回(すぐにとは限らないが)に要再実験だ。ただ使っている感覚では、まずピントがきちんと合わないような気がする。うーん、難しそうだ。それに、今回の実験はローパスのフィルター部分をなくしたものでなければならなかったようにも思う。ならば、FinePix700を使うのはマズイ(直すのメンドクサイから)。どうしたものか。
2000-01-30[n年前へ]
■ソフマップでお買い物 
磁界の可視化とバーコード
前回、
で「マグネビュアー」を使って磁界の可視化をして遊んでみた。今回はその続きである。ソフマップの磁気カードの中に書き込まれている磁気データを可視化して調べてみるのである。磁気カードには、
- 銀行のキャッシュカード
- クレジットカード
- テレホンカード
- オレンジカード
まずは、ソフマップカードの写真を示してみよう。これがソフマップで買い物をするたびにお世話になるソフマップカードである。
 |
この写真からではどこにデータが書き込まれているのかわからない。そこで、「マグネビュアー」の登場と言いたいところであるが、残念ながら今回は「マグネビュアー」は登場しないのである。「マグネビュアー」はとても便利なのであるが、さすがに磁気カードの磁気データを読もうとすると分解能が不足する恐れがある。
そこで、代打選手に登場願うことにした。代打選手はキヤノン製のLBPのトナーである。以前、
の時に「トナーはクーロン力で制御されて画像を作るのだ」という話があった。キヤノン製の白黒のLBPではクーロン力に加えて磁気力を使ってトナーを制御している。なので、キヤノン製の白黒トナーは磁性体粉末ということになる。テレホンカードが出た頃はキヤノン製のトナーを使ってデータを読み出していた人も多いはずである。みな、テレホンカードの表面を削りトナーを振り掛けていたのである。というのは、聞いた話であり、実体験に基づくものでは絶対にない。神に誓っても良い。その頃にキヤノン製のトナーを使い倒していたということは絶対にないのである。しかも、その数年後に(以下略)。
それでは、磁性体の微少粉末であるトナーをソフマップカードに振り掛けてみよう。
 |
ソフマップカードの磁気データが可視化されたのがわかると思う。磁気によるバーコードが見えるだろう。これがソフマップカードに書き込まれている磁気データである。
とはいえ、トナーの付着具合にムラがある。それは私が雑に実験を行ったからである。こんなにムラがあっても磁気コードが判別できるかどうか疑問を持たれる方も多いと思う。しかし、
- 読む方向に対して垂直な線が多い
- 読む方向に対して水平な線は少ない
そのようにして、ノイズを減らし、S/N比を上げた画像を示してみる。
どうだろうか、驚くほど綺麗になっているのがわかると思う。まさか、と思われるかもしれないが本当である。
さて、これはソフマップカードの磁気データの全体像であるが、もう少し拡大したものを以下に示す。
 |
極めて明瞭に磁気データが可視化されているのがわかると思う。これはトナーを振りかけて、1万円ちょっとのスキャナ(CanonのUSB接続の安物スキャナ)で読み込んだものに対して先の処理をしただけである。これほど明瞭になるのも、全て1次元バーコードの特徴のおかげである。磁気ヘッドの制作などをしなくても良いのである。
磁気カードの記録密度は銀行統一仕様(NTT)でもISO3554でも8.3bit/mm=211bit/inchであるから、最近の600dpi(dot/inch)程度のスキャナーであれば十分磁気データの画像読みとりが可能である。
それでは、もっと拡大してみる。拡大する部分は上の画像の右の辺りである。すると、このようになる。
 |
データ間隔がわかりやすいように、ここでは矢印や文字を書き入れている。この画像を見ると、磁気データは規則的な細かい周期性を持ち、その周期でいうと8つ単位でさらなる周期性があるように思われる。つまり、8bitをひとまとまりとしたデータが書き込まれているように見える。例えば、上の画像では
- ( 白、白、白、白、白、白、黒、黒 ) x 2
- ( 00000011 ) x 2
- ( ああああああたた ) x 2
複数枚のカードのこの部分を比較してみれば、比較的容易にデータ構造は解析することができるだろう。また、一枚のカードからでもカード番号などの数字と磁気データを比較することにより、解析することはやはり困難無しに解析できると思うのである。と、思うわけではあるが、あまりやりすぎるのはマズイと思われるので、今回はこれまでにしておく。