1999-01-08[n年前へ]
■2項分布のムラについて考える 
今回の目的を説明するために、少し準備を行う。
まず、2048個の[ランダムに0から256の値を持つもの]からなる1次元データを作成する。以下の左図がそのデータである。ここで、X軸がデータの順番であり、1から2048までを示し、Y軸がデータの値である。Y軸の数値ラベルは0から256の値である。折れ線グラフの方が1次元データとして実感できるのだが、そうすると真っ黒になってしまうので、点プロットグラフにしてある。
また、[0から256]のデータの出現頻度のグラフ(つまりヒストグラム)を右の図として示す。
 | 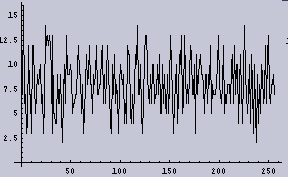 |
右のグラフを見ると、下は2回から上は15回位の間で出現頻度がばらついている。その頻度のムラは分散として計算することができる。今回の場合は2項分布である。
今回の目的は、そのムラを考えることである。広い範囲で見たときには、どの程度フラットだろうか。例えば、最初の100個のデータの平均と、次の100個のデータの平均というのはどの程度同じだろうか。それが1000個ならどうだろうか。1000個平均してみても場所によって、平均値はばらついているだろうか。もし、ばらついているとしたら、2項分布の確率過程を導入すると、広い範囲で見てみても認識できるくらいのばらつきを導入していることになる。その「ばらつき=ムラ」を人間が感じないためには、どの程度まで平均しなければならないのか。そういったことである。
ここで、先の2048個の1次元データは2048dpiの1次元画像データである、ということにしてみる。したがって、X軸の領域はトータル1inchを示すことになる。そして、以下の作業をする。
- 2048dpiの1次元画像データを2値化(128でしきい値とした)したものを8個に分断する。
- それぞれ、分断したデータ(256個)内で平均を取る。そなわち、8ppi(pixelper inch)の1次元データができる。
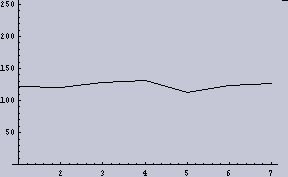 |  |
すると、2048dpiの(1/2の確率で2値化された)データというものは、今回の目的である「ムラを感じないための条件」を満たしていないということになる。ここでは画像に例えているが、別に画像だけの話ではない。
それでは、いくつか条件を振ってみたい。各々の条件下で示すグラフの領域は以下を示す。
| オリジナルの1次元データ | 左のヒストグラム。条件違いで軸が揃ってないのに注意。 |
| 8ppiに変換したもの Y軸はいずれも相対値であることに注意。Max=256と読み直す。 | 左のヒストグラム X軸はいずれも相対値であることに注意。Max=256と読み直す。 |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
オリジナルの1次元データ | 左のヒストグラム |
8ppiに変換したもの | 左のヒストグラム |
上の右下で出ているようなヒストグラムが2項分布であることは、サンプルを多く(しかし、試行回数を少なく)すればよくわかる。例えば、このようになる。
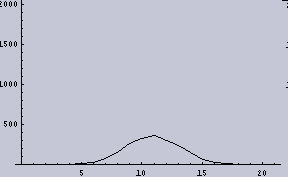

今回の話はあることの前準備なので、これだけでは話しが全く見えないかもしれない。というわけで、
1999-07-14[n年前へ]
■夏目漱石は温泉がお好き? 
文章構造を可視化するソフトをつくる
先週は新宿で開催されていた可視化情報シンポジウム'99を見ていた。参加者の世界が狭い(ジャンルが狭いという意味ではない)し、学生の発表が多すぎるように思ったが、少なくとも本WEBのようなサイトで遊ぶには面白い話もあった。というわけで、これから何回か「可視化情報シンポジウム'99」記念の話が続くかもしれない。とりあえず、今回は「小説構造を可視化しよう」という話だ。
まずは、「可視化情報シンポジウム'99」の発表の中から一番笑わせて(笑ったのはいい意味ですよ。決して皮肉ではないですよ。しつこいようですが、ホントホント。私のツボに見事にはまったのだからしょうがない。)もらった発表のタイトルはこれである。
文学作品における文体構造の可視化 - 宮沢賢治「銀河鉄道の夜」の解析-
白百合女子大学大学院の金田氏らによる発表だ。予稿集から、その面白さを抜き出してみよう。まずは過去の研究の紹介をしている部分だ。
作品(hirax注:夏目漱石の「虞美人草」と「草枕」)の始まりから終わりまでを時系列で捉えると(hirax注:話法に関する解析をすると)、二作品はともに円環構造、つまり螺旋構造を描きながら、物語が進行していくことが、四次元空間上に表現された。
中略
これは、作品の解析結果を可視化することで、夏目漱石の思考パターンと内面の揺れが明らかにされたことを意味する。
なんて、面白いんだ。この文章自体がファンタジーである。こういうネタでタノシメル人にワタシハナリタイ。おっと、つい宮沢賢治口調になってしまった。そして、今回の発表の内容自体は、宮沢賢治の「銀河鉄道の夜」の中に出てくる単語、「ジョバンニ・カンパネルラ・二」という三つの出現分布を調べて構成を可視化してみよう、そしてその文学的観点を探ろう、という内容だ。
本サイトは実践するのを基本としている。同じように遊んでみたい。まずは、そのためのプログラムを作りたい。名づけて"WordFreq"。文章中の単語の出現分布を解析し可視化するソフトウェアである。単語検索ルーチンにはbmonkey氏の正規表現を使った文字列探索/操作コンポーネント集ver0.16を使用している。
ダウンロードはこちらだ。もちろんフリーウェアだ。しかし、バグがまだある。例えば出現平均値の計算がおかしい。時間が出来次第直すつもりだ。平均睡眠時間5時間が一月続いた頭の中は、どうやらバグにとって居心地が良いようなのだ。
wordfreq.lzh 336kB バグ有り版
バグ取りをしたものは以下だ(1999.07.22)。とりあえず、まだ上のプログラムは削除しないでおく。
失楽園殺人事件の犯人を探せ - 文章構造可視化ソフトのバグを取れ - (1999.07.22)
動作画面はこんな感じだ。「ファイル読みこみ」ボタンでテキストファイルを読みこんで、検索単語を指定して、「解析」ボタンを押すだけだ。そうすれば、赤いマークでキーワードの出現個所が示される。左の縦軸は1行(改行まで)辺りの出現個数だ。そして、横軸は文章の行番号である。すなわち、左が文章の始めであり、右が文章の終わりだ。一文ではなく一行(しかもコンピュータ内部の物理的な)単位の解析であることに注意が必要だ。あくまで、改行までが一行である。表示としての一行を意味するものではない。なお、後述の木村功氏から、「それは国語的にいうとパラグラフ(段落)である。」という助言を頂いている。であるから、国語用の解析を行うときには「行」は「段落」と読み替えて欲しい。また、改行だけの個所には注意が必要だ。それも「一行」と解釈するからである。
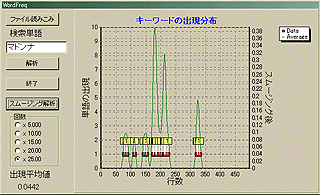 |
「スムージング解析」ボタンを押せば、その出現分布をスムージングした上で、1行辺りに「キーワード」がどの程度出現しているかを解析する。
そう、この文章は長い文章の中でどのように特定の単語が出現するか解析してくれるのである。
それでは、試しに使ってみよう。まずは、結構好きな夏目漱石の小説で試してみたい。
電脳居士@木村功のホームページ
から、「ホトトギス」版 「坊っちやん」のテキストを手に入れる。そして解析をしてみよう。まずは、この画面は夏目漱石の「坊っちやん」の中で「マドンナ」という単語がどのような出現分布であるかを解析したものである。
 |
文章の中ほどで「マドンナ」は登場してくるが、それほど重要なキャラクターでないことがわかる(このソフトがそう言っているんで、私が言っているのではない。だから、文句メールは送らないで欲しい)。
それでは、「湯」というキーワードで解析してみよう。「坊っちやん」と言えば道後温泉であるからだ。
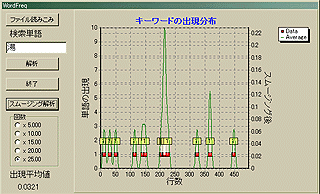 |
おやおや、「マドンナ」よりもよっぽどコンスタント(安定して、という意味で)に「湯」という単語は出現するではないか。出現平均値は「マドンナ」の方が多いが、安定度では「湯」の方が上だ。夏目漱石は「マドンナ」よりも「湯」すなわち温泉によっぽど興味があるようだ。
主人公を育てた重要人物「清」を調べてみると、こんな感じだ。
 |
小説の初めなんか出ずっぱりである。あと小説のラストにも登場している。
どうだろうか。見事に小説の可視化に成功しているだろう。結構、この解析は面白い。すごく簡単なのである。
これから新聞、WEB、小説、ありとあらゆる文章を可視化し、構造解析していくつもりだ。みなさんも、このソフトを使って面白い解析をしてみるとよいのではないだろうか? とりあえず、高校(もしかしたら大学の教養)の文学のレポートくらいは簡単に書けそうである。もし、それで単位が取れたならば、メールの一本でも送って欲しい。
というわけで、今回はソフトの紹介入門編というわけで、この辺りで終わりにしたいと思う。
1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
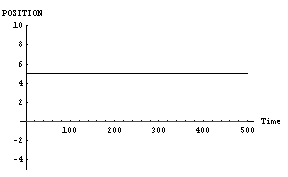
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
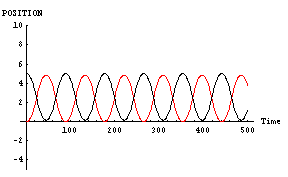 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
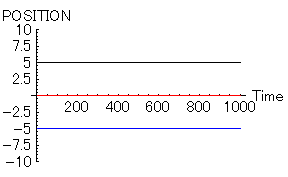
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
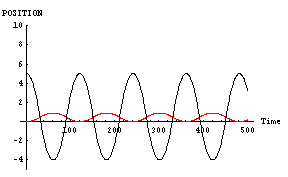 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
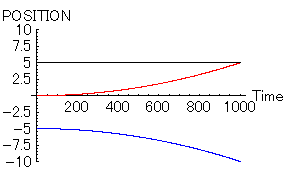
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
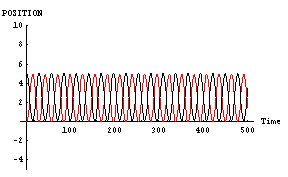 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
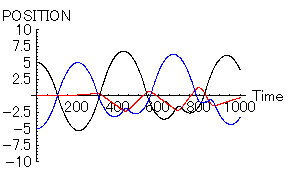
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-03-29[n年前へ]
■明日、春が来たら 
風の中の瞳

昨日、海辺を歩いた。車は海沿いの堤防の上に停めた。堤防の上に留めた車の揺れが止まらない程、強い風が吹いていた。もう三月も終わりなので、春一番というわけではないだろう。それでも、もう春なのだなぁ、と強く感じさせる。
ところで、この海辺からは富士山がよく見える。富士山レーダーもよく見える。この海辺ももちろん見通しは良いのだが、「見通せる範囲」を言うなら、富士山レーダーの方がずっと広い。遠くを見通すのがレーダーの使命なのだから、当たり前の話だ。そして、富士山の山頂から、遙か遠くまで見通し続けたのが、富士山レーダーである。
今日、NHKの「挑戦者たち」でその建設をした人達が紹介されていた。富士山レーダーを作る指揮をし、情熱を傾けていたのが当時、気象庁観測部補佐官だった藤原寛人、すなわち、新田次郎であるとは知らなかった。新田次郎が富士山の山頂に行きたいから気象庁に入ったというのは、知っていたが、富士山レーダー建設の指揮をしていたとは知らなかった。とても面白く、そして何故か納得する話だ。
息子の藤原正彦もそうだが、新田次郎の書く文章には「冷静に見通す力」と「情熱」が同居している。時々、新技術を考えていると、彼らのような、未来すなわち明日を「見通す力」と「それを手に入れる情熱」が欲しい、とつくづく思う。