1998-12-17[n年前へ]
■俺のドメイン 
オレの.コム
以前から、自分用ののドメインを取得したいとは思っていた。しかし、どこのバーチャルドメインにするかなど、決め手がなく何もしないでいた。しかし、今日、(いいかな?と思っていた)hirax.comをチェックしてみると、先週付けで取得されてしまっている。これではまるで、「物理の散歩道」の-ロバは何故死んだ-である。
ちなみに、-ロバは何故死んだ-とは次のような話である。
お腹を空かせたロバからちょうど等距離の所に2つのえさがある。完全に等距離なので、ロバはどちらのえさの方へ行ったら良いのかわからない。結局、ロバは餓死してしまうという話である。
今回の場合はhirax.comが取られてしまったことで、バランスは崩れたことになる。そこで、hirax.netを取得することにした。ついでに、internic(http://www.internic.net/)でいくつかドメインの作成日を調べてみた。現在では、toyota.comもsuzuki.comもどちらも自動車会社の管理になっているが、取得されたのは割に最近のようだ。最初に登録したのは誰だろうか。
私は好きではないが、小室哲哉のドメインkomuro.comもある。同じような線を調べてみると、speed.comは今年の9月末である。これなど、残っていたのが意外でもある。
私の好きな「種ともこ」tane.com(種とこもとは無関係だが)は96年である。同じくsmap.comも96年だ。smap.comのドメイン保持者はもちろん日本人である。ジャニーズファンは速いのかとも思ったが、そういうわけでもないようだ。v6.comは98年9月である。tokio.comもほんの2ヶ月前だ。hirosue.comは97年だ。強力なファンが管理しているようだ。 ところで、"hirosue.net"は空いていることに気づいた。ファンの方はどうだろうか。今なら空いている。
また、もっと素晴らしいドメインがある。「俺の、ドメイン」、すなわち、「俺の、コム」oreno.comである。バリエーションとして、「俺が、コム」orenga.com、「俺は、コム」oreha.com等がある。このいずれもが、まだ取得されていない。こんな素晴らしいドメインを取らなくてどうするのだろう。
「オレの、コム」と言ってみたいではないか。
上までを書いてから数日後、日本人以外の「俺のコム」といいたい奴がいるかもしれないと思い、www.my.comにアクセスしてみて驚いた。ぜひ、
www.my.com
にアクセスしてもらいたい。びっくりすると思う。
BEATLES.COM Record created on 29-Apr-95.JAPAN.COM Record created on 01-Nov-94.APPLE.COM Record created on 19-Feb-87.BASEBALL.COM Record created on 20-May-97.SUN.COM Record created on 19-Mar-86.HIRAX.COM Record created on 10-Dec-98.SUZUKI.COM Record created on 14-May-96.TOYOTA.COM Record created on 29-Dec-94.USA.COM Record created on 03-Nov-93.IBM.COM Record created on 19-Mar-86.KOMURO.COM Record created on 01-Dec-95.SPEED.COM Record created on 22-Sep-98.TANE.COM Record created on 26-Jun-96.SMAP.COM Record created on 03-May-96.HIROSUE.COM Record created on 25-Nov-97.V6.COM Record created on 23-Sep-98.TOKIO.COM Record created on 31-Oct-98.
1999-01-10[n年前へ]
■宇宙人はどこにいる? 
画像復元を勉強してみたい その1
知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。
ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。
 |  |
 |  |
画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。
(式:1) 画像:4 = 画像:3 * 画像:2
画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。
このようなごく単純な場合には
(式:2) 画像:3 = 画像:4 * (1/画像:2)
とすれば、画像:3を復元できることになる。
そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。
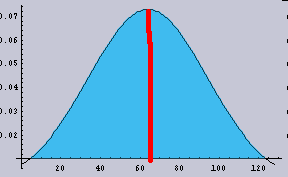 |
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。
 | 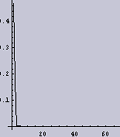 |
それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。
 |  |
逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))
= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)
とやると、次のデータが得られる。
 |
(式:2) 画像:3 = 画像:4 * (1/画像:2)
を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。
そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。
この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。
Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像
Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)
である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。
これを使って復元してみたのが、次のデータである。
 |
まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。
 |
 |  |
 |
その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。
関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか?売れると思うんだけど。新書版は高すぎる。
宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。
さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で
地球外生命体は存在するのか?( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )
という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。
1999-02-26[n年前へ]
■ヒトは電磁波の振動方向を見ることができるか? 
はい。ハイディンガーのブラシをご覧下さい
(1999.02.26)
リチャード・ファインマンの本の中で次のような問題があったように思う。
「偏光板がフィルターが一枚だけある。その偏光フィルターの偏光方向をどのようにして知れば良いか?」
その本の中での答えは、
「物体の反射光を偏光フィルターを通して見てみる。」
だった。ブルースター角で入射した光の反射光は、入射面に対して電場の振動方向が垂直になっている、ということを利用するわけである。
分かりやすいように、偏光フィルターを通してみたガラスの反射光をデジカメで撮影してみる。左が反射光を通すような角度に偏光フィルターを回したものであり、右が反射光をカットするような角度に偏光フィルターを回した場合である。この左の場合、すなわち、反射光が一番通過している角度から液晶の偏光面がわかるわけである。
 |  |
ところで、このようなファインマンが示したような方法を用いなくても、そもそもヒトは電磁波の振動方向を見ることができるのである。以前、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「鳥は太陽の位置、光の偏光パターンを位置のセンサーに使う」という話があった。ヒトも同じく光の偏光方向、すなわち、電磁波の振動方向を見ることができるのである。鳥はどう見えるかは私にはわからないが、ヒトならば自らが実験台になれるので、電磁波振動方向をどう見ることができるか調べてみたい。というわけで、「渡り鳥の秘密- 3000kmの彼方へ - (1999.01.30) 」の中で「近日中にある実験をする予定である」と書いたものが今回の確認実験である。なお、光の進行方向と磁界の振動方向を含む面を「偏光面」、電界の振動面を含む面を「振動面」と呼ぶ。
電磁波の振動方向をヒトが見ると「ハイディンガーのブラシ "Haidinger'sBrushes"」というものが見える。それを知ったのは、いつものごとく「物理の散歩道」からである。網膜に複屈折性があるために「ハイディンガーのブラシ」が見えるのだという。
私はこれまで、「ハイディンガーのブラシ "Haidinger's Brushes"」を見たことがない。いや、正確に言えば意識したことがない。そこで、判別しやすいように直線偏光を用意してやることにした。そこで、東急ハンズで偏光フィルターを買ってきた。
そして、空を見てみる。もちろん、偏光の偏りが強い、太陽を中心にして90度の角度をなす同心円方向である。詳しくは、
- 可視-赤外域での偏光観測による衛星観測手法の開発基礎研究(http://www.mri-jma.go.jp/Dep/sa/Lab1/labt01-s.html)
- エアロゾル観測(http://mars.im.kindai.ac.jp/KISYO/YPROJECT/kansoku.html)
さて、ヒトである私は、空を眺めて格闘すること5分程で、「ハイディンガーのブラシ"Haidinger's Brushes"」がわかるようになった。私が見たハイディンガーのブラシ"Haidinger's Brushes"を示す。
 |
この絵で太陽の方向は右上であり、偏光面は次の絵の青の矢印方向になる。
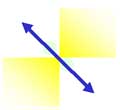 |
というわけで、ヒト(少なくとも私は)電磁波の振動方向を見ることができるのである。慣れてしまうと、白い紙を見つめているときなども(条件によっては)見えるようになる。色を扱う人は意識すると面白いと思う。
ところで、偏光フィルターがどういうものか知らない人のために、NotePCの液晶に偏光フィルターを重ねた写真を示す。
 |  |
なぜ、こうなるかわからない方は、
などを参考にして欲しい。液晶ディスプレイの構造がわかると思う。そして、面白いことに気づいた。NotePCの液晶からの光は直線偏光である。ということは、NotePCの液晶にはハイディンガーのブラシが映っているのである。正確に言えば、NotePCの液晶を見ているあなたの視界の中央には、ハイディンガーのブラシが映っているのである。と、気づいてみると確かに見えている。
というわけで、液晶ディスプレイを使用している方はハイディンガーのブラシを見て頂きたい。以下のやり方がわかりやすいと思う。
1.このWindowを最大化する
2.下へスクロールして画面を真っ白にする。
3.液晶ディスプレイ(NotePC)を回転させる。
4.画面(視点)の中央に(視点に対して位置が)動かない黄色いもやが見えるはず。もちろん、回転はする。
液晶ディスプレイやヘッドマウントディスプレイ(HMD)を色々見てみたが、どれにもハイディンガーのブラシは存在していた。視界の中央に不思議な十字架のように現れているのである。現代の液晶技術が負う十字架である。
誰もが、目の前にあるのにそれに気づかないというのも、実に面白い。まるで、「青い鳥」のようである。そして、そういうことはとても多いのではないかと思う。それはそれで面白い話だ。
- それでは、ハイディンガーのブラシをご覧下さい -
1999-03-28[n年前へ]
■ハードディスクのエントロピーは増大するか? 
デフラグと突然変異の共通点
fjでKByteの定義(よく言われる話だが)が話題になっていた。「なんで1024Byteが1KByteなんですか」というものである。そのスレッドの中で、
- 整数値だけでなく、分数値のbitもある
- 1bitのエントロピーも定義できるはずで、それならハードディスクは結構エントロピーを持つかも
初めに、「整数値だけでなく、分数値のbitもある」という方は簡単である。{0,1}どちらかであるような状態は1bitあれば表現できる。{0,1,2,3}の4通りある状態なら2bitあれば表現できる。{0,1,2,3,4,5,6,7}までなら3bitあればいい。それでは、サイコロのような状態が6通りあるものはどうだろうか? これまでの延長で行くならば、2bitと3bitの中間であることはわかる。2進数の仕組みなどを考えれば、答えをNbitとするならば、2^N=6であるから、log_2 ^6で2.58496bitとなる。2.58496bitあれば表現できるわけだ。
後の「1bitのエントロピーも定義できるはず」というのはちょっと違うような気もする。そもそもエントロピーの単位にもbitは使われるからだ。しかし、ハードディスクのエントロピーというのはとても面白い考えだと思う。
そこで、ハードディスクのエントロピーを調べてみたい。
次のような状態を考えていくことにする。
- きれいにハードディスクがフォーマットされている状態。
- ハードディスクの内容が画像、テキストファイル、圧縮ファイル、未使用部分に別れる。
- その上、フラグメントが生じる。
画像ファイル、テキストファイル、圧縮ファイル、未使用部分を1Byteグレイ画像データとして可視化してみる。
 |  |  |  |
ところで、このような可視化をすると、ファイルの種類による差がよくわかる。てんでばらばらに見えるものは冗長性が低いのである。逆に同じ色が続くようなものは冗長性が高い。こうしてみると、LZH圧縮ファイルの冗長性が極めて低いことがよくわかる。逆に日本語テキストデータは冗長性が高い。もちろん、単純な画像はそれ以上である。
それでは、これらのようなファイルがハードディスクに格納された状態を考える。
- きれいにハードディスクがフォーマットされている状態。
- ハードディスクの内容が画像、テキストファイル、圧縮ファイル、未使用部分に別れる。
- その上、フラグメントが生じる。
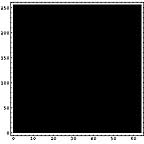 | 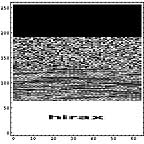 | 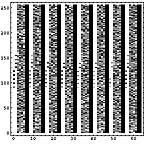 |
横方向の1ライン分を一区画と考える。ハードディスクならセクタといったところか。その区画内でのヒストグラムを計算すると以下のようになる。この図では横方向が0から255までの存在量を示し、縦方向は区画を示している。
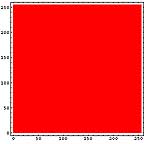 |  |  |
LZH圧縮ファイル部分では0から255までのデータがかなり均等に出現しているのがわかる。日本語テキストデータなどでは出現頻度の高いものが存在しているのがわかる。
それでは、無記憶情報源(Zero-memory Source)モデルに基づいて、各区画毎のエントロピーを計算してみる。
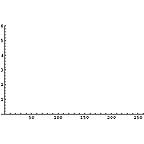 |  |  |
これを見ると次のようなことがわかる。
- 未使用ハードディスクは全区画にわたりエントロピーは0である
- 3種類のファイルが格納された状態では、それぞれエントロピーの状態が違う。
- 画像ファイルでは複雑な画像部分がエントロピーが高い
- 日本語テキストファイル部分は結構エントロピーが高い。
- LZH圧縮ファイル部分はエントロピーが高い。
- フラグメントが生じると、トータルではエントロピーが高くなる。
- しかし、平均的に先のLZH圧縮ファイル部分の状態よりは低い。
0 | 691.28 | 982.139 |
というわけで、今回の結論
「ハードディスクのエントロピーは増大する。」
が導き出される。もし、ハードディスクのデフラグメントを行えば、エントロピーは減少することになる。
こういった情報理論を作り上げた人と言えば、Shannonなのであろうが、Shannonの本が見つからなかったので、今回はWienerの"CYBERNETICS"を下に示す。もう40年位の昔の本ということになる。その流れを汲む「物理の散歩道」などもその時代の本だ。
 |
生物とエントロピーの関係に初めて言及したのはシュレディンガーだと言う。ハードディスクと同じく、企業や社会の中でもエントロピーは増大するしていくだろう。突然変異(あるいは、ハードディスクで言えばデフラグメント)のような現象が起きて、エントロピーが減少しない限り、熱的死(いや企業や会社であれば画一化、平凡化、そして、衰退だろうか)を迎えてしまうのだろう。
1999-06-28[n年前へ]
■風呂場の水滴を考える。 
オールヌードの研究員
風呂場の天井から浴槽めがけて、水滴がしたたって音がしているのはよくある風景である。ピーンという(もちろん人によっても印象は違うのだろうが)気持ちのいい音がしている。似たようなものとしては、水琴窟などもある。この音がなぜ鳴るかは、ロゲルギストの「物理の散歩道」に詳しい考察がある。それによれば、水滴が一粒落ちたように見えても、実は何粒かに別れており、ちょうどカルガモの親子のようになっているという。つまり、大きな親の水滴の一粒の後を、何粒かの小さな子どもの水滴が追いかけているという具合である。まず、水滴の親が水面に空洞をつくり、その中に子どもの水滴が飛び込むことにより音が出るという。結局、水滴の音を作っているのは、その子どもの水滴の方だという。「物理の散歩道」の中では、針をつたって水滴を落とせば、子どもの水滴ができないという。
風呂に入って、濡らした手から水滴を落としてみる。指の爪の先から水滴を落とすと音はほとんどしないが、指の「はら」から落とすと派手に音がする。ぜひ、自分でも確かめていただきたい。
爪先は比較的尖っているので、落ちる水滴は一粒だが、比較的平らな指の「はら」からの場合には、カルガモ親子のような水滴が落ちているせいだろう。
なぜ、このような違いが生じるかを推測してみたい。まずは、下の絵を見て欲しい。
 |  |
上の上手な絵が言いたいのは、次のような推測である。
- 平らな表面から水滴が落ちる際には、長く伸びた水のブリッジが出来ていて、1つぶ目の水滴が落ちた後も、このブリッジ部分が「カルガモの子ども」のように小さな水滴となって後を追いかけていくのではないか。
- それに対して、尖った表面から水滴が落ちる際には、先のブリッジ部分のほとんどは水でないため、後続の水滴は発生しない。
計算モデルとしてどのようなものを使うかであるが、私の知っている範囲では大きく分けて2種類のやり方がある。
- 流体をモデル計算する。すなわち、Navier-Stokesの方程式を解く。
- 流体を粒子のようなものの連続体として解く(ex.格子ボルツマン法)
電気通信大学情報工学科情報数理工学講座渡辺研究室( http://assam.im.uec.ac.jp/fluid.html )
 |
また、水滴が水面に衝突する状態の計算は、電気通信大学情報工学科情報数理工学講座渡辺研究室にもあるし、他にもNaSt2DというFreeの2次元Navier-Stokes方程式のソルバーを用いて行われた計算結果が
http://www5.informatik.tu-muenchen.de/forschung/visualisierung/praktikum.html
にある。
 |
Michael Griebel氏らによるNast2Dのコードは公開されているので、その中身をいじりながら、計算を行う予定である。
とりあえず、今回はバックグラウンドを紹介する所までで、次回(といってもすぐではないだろう)に計算の本番に入りたい。
手のひらの実験から考えると、風呂場で水滴の音が聞こえるのは天井が平らなせいだということになる。ならば、鍾乳石のようなつらら形状の天井の風呂場では音がしないのだろうか?しかし、水滴は空気中で落下していく最中には空気の抵抗をうける。そのため、大きな水滴は落ちる最中に分裂し、複数の水滴になってしまう。
となると、
- 落ちる水滴の最初の大きさは、どう決まっているのか。
- 水滴は落下するスピード、水滴の大きさがどの程度になると分裂するのか?
ところで、インクジェット方式のカラープリンターも液滴で画像を描くのだから、液滴の様子は重要な筈である。液滴が飛び散ってしまっては困るし、位置がずれても困る。各社ともカルガモの子ども水滴をなくすために色々工夫をこらしている筈だ。
実は風呂場の水滴問題は重要で、奥が深いのだ。オールヌードで私は考えるのであった。