1999-03-28[n年前へ]
■ハードディスクのエントロピーは増大するか? 
デフラグと突然変異の共通点
fjでKByteの定義(よく言われる話だが)が話題になっていた。「なんで1024Byteが1KByteなんですか」というものである。そのスレッドの中で、
- 整数値だけでなく、分数値のbitもある
- 1bitのエントロピーも定義できるはずで、それならハードディスクは結構エントロピーを持つかも
初めに、「整数値だけでなく、分数値のbitもある」という方は簡単である。{0,1}どちらかであるような状態は1bitあれば表現できる。{0,1,2,3}の4通りある状態なら2bitあれば表現できる。{0,1,2,3,4,5,6,7}までなら3bitあればいい。それでは、サイコロのような状態が6通りあるものはどうだろうか? これまでの延長で行くならば、2bitと3bitの中間であることはわかる。2進数の仕組みなどを考えれば、答えをNbitとするならば、2^N=6であるから、log_2 ^6で2.58496bitとなる。2.58496bitあれば表現できるわけだ。
後の「1bitのエントロピーも定義できるはず」というのはちょっと違うような気もする。そもそもエントロピーの単位にもbitは使われるからだ。しかし、ハードディスクのエントロピーというのはとても面白い考えだと思う。
そこで、ハードディスクのエントロピーを調べてみたい。
次のような状態を考えていくことにする。
- きれいにハードディスクがフォーマットされている状態。
- ハードディスクの内容が画像、テキストファイル、圧縮ファイル、未使用部分に別れる。
- その上、フラグメントが生じる。
画像ファイル、テキストファイル、圧縮ファイル、未使用部分を1Byteグレイ画像データとして可視化してみる。
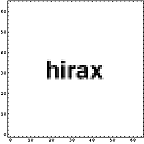 |  |  |  |
ところで、このような可視化をすると、ファイルの種類による差がよくわかる。てんでばらばらに見えるものは冗長性が低いのである。逆に同じ色が続くようなものは冗長性が高い。こうしてみると、LZH圧縮ファイルの冗長性が極めて低いことがよくわかる。逆に日本語テキストデータは冗長性が高い。もちろん、単純な画像はそれ以上である。
それでは、これらのようなファイルがハードディスクに格納された状態を考える。
- きれいにハードディスクがフォーマットされている状態。
- ハードディスクの内容が画像、テキストファイル、圧縮ファイル、未使用部分に別れる。
- その上、フラグメントが生じる。
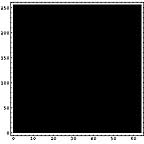 | 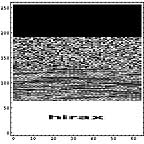 | 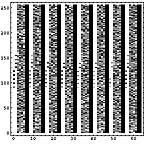 |
横方向の1ライン分を一区画と考える。ハードディスクならセクタといったところか。その区画内でのヒストグラムを計算すると以下のようになる。この図では横方向が0から255までの存在量を示し、縦方向は区画を示している。
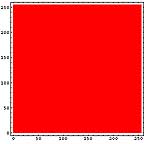 |  |  |
LZH圧縮ファイル部分では0から255までのデータがかなり均等に出現しているのがわかる。日本語テキストデータなどでは出現頻度の高いものが存在しているのがわかる。
それでは、無記憶情報源(Zero-memory Source)モデルに基づいて、各区画毎のエントロピーを計算してみる。
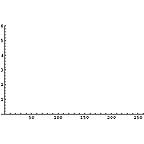 |  |  |
これを見ると次のようなことがわかる。
- 未使用ハードディスクは全区画にわたりエントロピーは0である
- 3種類のファイルが格納された状態では、それぞれエントロピーの状態が違う。
- 画像ファイルでは複雑な画像部分がエントロピーが高い
- 日本語テキストファイル部分は結構エントロピーが高い。
- LZH圧縮ファイル部分はエントロピーが高い。
- フラグメントが生じると、トータルではエントロピーが高くなる。
- しかし、平均的に先のLZH圧縮ファイル部分の状態よりは低い。
0 | 691.28 | 982.139 |
というわけで、今回の結論
「ハードディスクのエントロピーは増大する。」
が導き出される。もし、ハードディスクのデフラグメントを行えば、エントロピーは減少することになる。
こういった情報理論を作り上げた人と言えば、Shannonなのであろうが、Shannonの本が見つからなかったので、今回はWienerの"CYBERNETICS"を下に示す。もう40年位の昔の本ということになる。その流れを汲む「物理の散歩道」などもその時代の本だ。
 |
生物とエントロピーの関係に初めて言及したのはシュレディンガーだと言う。ハードディスクと同じく、企業や社会の中でもエントロピーは増大するしていくだろう。突然変異(あるいは、ハードディスクで言えばデフラグメント)のような現象が起きて、エントロピーが減少しない限り、熱的死(いや企業や会社であれば画一化、平凡化、そして、衰退だろうか)を迎えてしまうのだろう。
1999-06-10[n年前へ]
■コピー機と微分演算子 
電子写真プロセスを分数階微分で解いてみよう
前回、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
の中で、電子写真プロセスは「画像のエッジ部分が黒くなり、そうでないソリッド部分は画像が飛びやすい... 画像のエッジ部分、すなわち、電位変化が大きく、電界強度の高い部分に対してトナーが現像されやすい... 」という文章がある。この脈絡は何か見覚えがないだろうか?そう、
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の中の、「人間が画像を感じる特性というものは、画像強度と画像強度変化(画像強度の一階微分)の中間的なものであると言うことができるかもしれない。」という文脈と似ている。また、「ゼロックス...」の回での(昔の)電子写真の特徴、
- エッジ強調される。
- 細かいところはボケてしまう。
参考までに、以前の話のときに用いた画像を示しておく。
まずは、
ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
における(昔の)モノクロコピーを模したものである。
 |  |
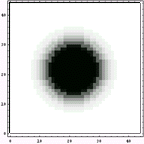
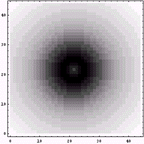
分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
の際に解析した元画像と0.75階画像である。ただし、この解析は2次元解析ではなく、1次元における計算を回転させて、中心対称な画像を作成している。その理由は前回述べたので今回は述べない。
 |  |
それでは、解析を始める。まずは、Photoshop5による「(昔の)コピー機シミュレーション」である
 |  |
次が、分数階微分画像だ。今回もMathematicaを用いて計算している。検算が終了したら、Notebookも公開予定だ(実は検算が終了していないのだ...)。
 | 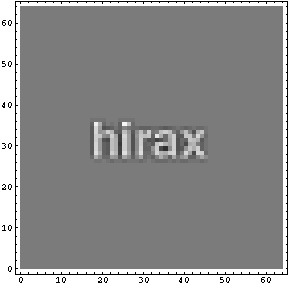 |
胸を張って「似ている」と断言するつもりはないが、少しは似ているのではないだろうか。別に似るまでがんばっても良いのだが、この分野の話はあまりやりすぎるわけにはいかないのである。ということで、強引ではあるが、今回の話の結論は「アナログコピーはオリジナルコピーの0.75階微分だ」というところで終わらせてもらう。
今回は、コピー機によるコピーを微分演算子と結びつけてみたわけだが、複数回のコピーに適用してみると面白いだろう。例えば、孫コピーは0.75+0.75階微分=1.5階微分であるとかだ。
また、同じ現像プロセスといっても色々あるわけであるから、各現像方式により微分演算子の階は異なるのが適当だろう。例えば、この機械は0.8階微分(つまりほとんどエッジ現像)であるが、こちらの機種は0.05階微分(極めて元画像に近い)で再現性に優れる、などという論議もできるかもしれない。
ところで、某所で今回の話と似て非なる話がCoffeeBreakとして公開されている。しかし、そちらは一般公開されていない。というわけで、今回は分数階微分の第3話ではなく、第4話ということになる。STARWARS風に言えば、Episode4だ。STAR WARSのようなSF映画もそうであるが、こういった話は生物(なまもの)である。ずっと置いておくと腐ってしまう。「腐ってこそ美味い食べ物もある」、という反論も聞こえてきそうだが、そういったものは少数の例外である。味オンチの料理人の作ったものではあるが、どうか賞味期間内に味わって頂きたい。
1999-10-18[n年前へ]
■沸点と数学の挑戦状 
みつからない「解決編」
| いったい、いつから疑問に思うことをやめてしまったのでしょうか? いつから、与えられたものに納得し、状況に納得し、色々なこと全てに納得してしまうようになってしまったのでしょうか? いつだって、どこでだって、謎はすぐ近くにあったのです。 何もスフィンクスの深遠な謎などではなくても、例えばどうしてリンゴは落ちるのか、どうしてカラスは鳴くのか、そんなささやかで、だけど本当は大切な謎はいくらでも日常にあふれていて、そして誰かが答えてくれるのを待っていたのです....。 加納朋子 ななつのこ より |
加納朋子の「ななつのこ」という小説を読んだ。創元推理文庫から出ているのだから、ミステリといっても良いだろう。私の好きな北村薫の「空飛ぶ馬」に始まる「円紫さんと私」シリーズによく似た雰囲気を持つ本である。
それを読んで、ふと思い出した。
私が通っていたM高校の話だ。M高校は武蔵野の玉川上水のほとりにある。
そのことを聞いたのは月曜の朝だ。日曜日の昼間に変質者が現れたというのである。目撃した人によれば、変質者は生徒用の上履きを履いていて、手には白い布を持っていたという。顔などはよくわからなかったそうだ。目撃者に驚いた変質者は逃げてしまい、白い布を落としていった、というのだ。
それだけなら、「単なる変な奴がいた」ということで話は終わった筈だ。問題は、その白い布に麻酔薬が含ませてあったという点だった。悪ふざけではすまない。
私は友人の鴨志田とその事件について話をしていた。気になることがあったからだ。変質者が目撃された場所が問題だったのだ。図に描くとこんな感じだ。
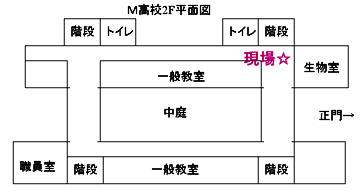 |
 |
そこは2階の中では職員室から一番遠い。一番校門に近い玄関を揚がった所である。そして、生物室の隣だった。
生物室は、普通の教室とは違う。通常は鍵がかかっているし、それは鍵がかけられるということでもある。
生物部の部長・副部長は生物室の鍵を使える立場にあった。そして、鴨志田は生物部の部長だった。
「変質者は生物室に出入りできる奴かな?」これはどうにも重大な問題だったのである。
「生物の部長・副部長経験者ってこと?」
「うーん。」
「麻酔薬ってクロロホルムとか、かな?」と鴨志田にぼくが言うと、「立て板に水」状態で、彼の推論を聞かせてくれた。
「いや、きっとエーテルだね。」なるほど説得力はある。いや、ありすぎるといっても良い程だ。コイツ、むちゃくちゃ怪しいヤツである。犯人候補No.1である。一朝一夕で考えた理屈とは思えない。
「今時、クロロホルムなんて使われていないんだよ。」
「副作用もあるしさ。」
「あと、沸点を考えてみろよ。」
「エーテル、つまりジエチルエーテルDiethyl Ether ( (C2H5)2O )は沸点が34.6℃だ。」
「それに対して、クロロホルムChloroform ( CHCl3 )は沸点が61.7℃だ。」
「ハンカチにクロロホルムを含ませて顔に当ててもなにもおきない。」
「だけど、エーテルは人間の顔にあてたら、体温のせいで瞬間的に気化するんだよ。」
「つまり、エーテルの気体で顔の周りが覆われるわけだ。」
「呼吸なんかしたらエーテルを吸わざるをえないだろ。」
「だから、クロロホルムとかよりエーテルのほうが、変な用途には向いているんじゃないかな。」
「もっとも、即座に気を失うとは思えないけどね。」
「そういうことって生物部の部員ならみんなわかるもの?」と聞くと、
「部長・副部長をやるくらいの人は確実にわかる。けど、他の人でもわかるやつはきっと多いよ。」また、部長・副部長経験者である。
「ところで、生物室にエーテルはある?」と訊くと、
「うん、あるよ。」とのお答え。やはり、生物室の「鍵」である。
「生物室に入れる人なら手に入ると思うよ。」
「せめて靴の先の色がわかれば。」そう靴の先の色は赤・黄・緑と色分けされており、それで1,2,3年生の区別がつくのだ。もっとも、それと関係ないサンダルを履いている人のほうが実際は多いのであるが。それに、靴を履いていたから学内の生徒とは限らないが。
「学年がわかるね。」
次に、ぼくらは覚えたばかりの数学の知識をひけらかす(まだ高校生だから)話をしていた。
犯人(変質者)の条件
- 男
- 生徒用の上履きを履いてた。
- 麻酔薬に関する知識がある。
- 麻酔薬を手に入れられる。
- 生物室に入れる。
- 一人
ここで、私は
「ぼくは生物室の鍵を持っていないから、必要条件を満たしていないな。」
つまり、「生物室に入れる=鍵を使える=生物の部長・副部長経験者」であるから、「ぼくは必要条件のひとつを満たしていない」と主張したのだが、鴨志田は聞き入れなかった。。
「オマエに鍵なんか必要ないだろう。」
そう、物理部の部長(私のこと)になるには「錠前破りが得意」でなければならなかったのである。すなわち、物理部の部長経験者であると「生物室に入れる。」ということの「十分条件」をもれなく手にしてしまうのである。イヤーなおまけである。もっとも、私は生物・化学は苦手であるので、必要条件を満たしていない。
一方犯人の「十分条件」を考えてみるとこんなものがある。
- 生物部の部長・副部長
 |
「ところで、こんなミステリがあったらどう思う? 探偵がめちゃくちゃ論理的なヤツでさ。」さてさて、普通ならばここに「読者への挑戦状」が入るところだろう。だから、この話にも入れてみる。ただ、少し定型とは違う。
「コンパクト群の表現論なんかで語られてさ。」
「犯人を指摘する所なんか、数式だらけな話。」
「作家はMathematicaをワープロ代わりにしててさ。」
「......なんか、一般受けしそうにないな...おれにすら面白くないぞ...」
| ここまでに、犯人を示す証拠が全ての証拠がそろっているとは思わないし、そもそも、犯人が登場しているかどうかすら私にはわからない。いや、実際のところ登場していないと100%確信している。しかし、名探偵のあなたなら、きっと犯人を指摘してくれるに違いない。私と鴨志田の懸念を吹き飛ばしてくれるに違いない、と思うのだ。 犯人は一体誰なのだ... |
1999-11-13[n年前へ]
■やっぱり、ウニが好き ! 
Dr.フラーはウニの夢を見るか?
私は野球は特に好きでも嫌いでもないが、野球場でビールを飲むのは大好きだ。と、始めると
の間違いと思われるかもしれない。しかし、それは違う。今回は、ウニとドームハウスの共通点について、考えてみたい。ただ、かなりビールが脳みそにしみているせいか、少しドンデモ話になるかもしれない。そこは、「ビックエッグの力学」と共通である。 私の中では、野球観戦と言えば、ビールだ。野球にはビールが良く似合う。そして、今現在も目の前にはビールがある。そして、寿司がある。といっても、スーパーで買った安物である。二つ合わせても1000円にしかならない。
 |  |
安物といっても、私の住んでいるのが港町だから安い、ということもある。何しろ、ほとんどのスーパーの魚売り場でイルカの肉なども置いてあるのだ。嘘ではない。ホントにホントである。私も、引っ越してきた当時はビックリしたが、本当である。アメリカの動物愛護団体が見たらびっくりの風景だろう。「イルカと人間はお友達」と言ってる人には見せられない風景だ。
あまりおいしそうではないので、私はまだ実際に味わってはいない。しかし、地元の人の中には「よく食べる」と言う人もいる。いつか、挑戦してみたい。
さて、上の写真で共通しているのはウニである。ウニと言えば、こんな姿をしている。
 |
「海栗」と書いてウニと読むことが実に納得できる姿である。しかし、内面はもう少し違う。実は、ウニはドームにそっくりである。前回考えたドーム球場ではないが、ウニは実はドーム構造をしているのだ。「そんなことは当たり前じゃないか」と言う人もいるだろう。しかし、私はつい最近までそれを知らなかった。そもそも、骨があるとすら思っていなかったのである。
もしかしたら、私のようにウニの内面を知らない人もいるかもしれない(そんな人はいない、という声も聞こえそうだが)。そこで、ウニの骨の写真を示してみる。下に示すのが、色々なウニの骨だ。
 実物はとてもきれい。日本古来の木工細工のような穴がとてもきれいである。 |
これは少し前に、宇宙科学研究所の黒谷氏の実験室を見学(ただ邪魔しただけという気もするのであるが)する機会があり、そのとき頂いたものである。最初に見たときは、「目からウロコ」であった。まさか、あの針の山の下にこんな頑丈な殻が存在しているとは、思わなかった。
写真ではわからないかもしれないが、骨には小さな穴が極めて規則的に開いている。それが、日本古来のとても出来がいい木工細工のようである。光に透かしてみると、うっとりするようなきれいさである。内部に強い光源でもおけば、プラネタリウムやミラーボールみたいに細い光線を放射する、きれいなアクセサリーができそうだ。
ところで、「何故、宇宙科学研究所の実験室にウニが?」と思われる方は、WEBで検索でもかけてみると良いかもしれない。「宇宙生物学」という面白い実験分野があるものだ。
例えば、無重力の中で生物がどのような挙動を示すか、などの研究をしたりするらしい。飛行機にのってそういう実験を繰り返すわけである。遊園地のフリーファールやバンジージャンプ、そして、ジェットコースターでさえ、駄目な私には地獄のような研究分野である。
さて、上の、ウニの骨の姿はまさにドームそのもの、とは思えないだろうか? そう、似ているのだ。 そっくりなのだ。試しに、このドームなどを見れば納得できるだろう。
 |
これは、富士山頂の厳しい環境を耐えるために、極めて安定なドーム構造が用いられているのだ。三角形のパネルが組み合わさるドームハウスは極めて頑丈である。ウニも、同じように頑丈なドーム構造の骨格を持っているのである。レーダードームは富士山頂で頑張っているが、宇宙科学研究所のウニは色々なところへ連れて行かれて、厳しい実験に耐えているのである。
こういった、ドームと言えば、R.バックミンスター・フラー博士のドーム理論だろう。フラー博士とドームハウスのスケッチ図を示してみる。
|
よく、環境適応性の高さを謳うことの多いドームハウスであるが、もしかしたら、ウニがその祖先であるかもしれない。もしかしたら、フラー博士は「海の中でじっとたたずむウニの夢を見て」ドームハウスを思いついたのかもしれない。
アメリカ人であるフラー博士がウニを食べたとは思えない、という人も多いだろう。それは確かにその通りである。しかし、フラー博士はかなりの変人である。変人ならば、ウニを食べまくっていたとしても、おかしくはない。
普段は「何を馬鹿な発想だ」と思うことだろう。しかし、ドーム球場の野球を見ながら、脳みそがビールとウニで満たされてしまうと、「そうだ、フラー博士はウニが大好きなのだ!そうに違いない!」と確信してしまうのだ。
仮に、フラー博士がウニに影響されていないとしても、ウニはフラー博士がドーム理論を考えるずっと太古の昔から、ドーム構造をしていたのである。ならば、「元祖はやはりウニなのだ!」と言ってしまって良いだろう。太古から厳しい環境を耐えつづけてきたウニは、今や宇宙へ飛び出し、さらに厳しい環境の中で活躍しているのである。
1999-12-12[n年前へ]
■色覚モドキソフトを作る(色弱と色空間その4) 
五十歩百歩
まず、先に書いておこう。今回は、
で作成したTrueColorと似たようなプログラムを作成してみたい。何しろ関係ない話が以降、長々と続くからである。昔から、科学者は「色」というキーワードに強く惹かれている、と思う。そんなことを私が思うまでもなく、量子色力学(quatumchromodynamics)、色つき空間群(Color-symmetry)等のキーワードにその事実は現れている。これらの言葉は普通に使われる「色」という言葉とは違う性質を表すものである。しかし、科学者が「色」というものを基本的なものであると感じているために、どんなものが対象でも、「性質」の代表的なものとして、「色」という言葉が連想されるのだろう。
私は学生時代の量子力学の授業のおかげで、「色」という言葉を聞くと今でも眠くなってしまうのである。何しろ、私の通う理学部の教室の横は農学部の畑だったのだ。教授の声と共に「モゥーーー」という牛の鳴き声が聞こえてくるのだ。教授の声と牛の鳴き声が絶妙のハーモニーとなるのである。ただでさえ眠くなるのに、そのハーモニーはクロロホルムもビックリの睡眠作用を発揮するのだ。私はそのハーモニーのおかげで何回も記憶を飛ばされた。
また、その牛達のおかげで、授業の中で「匂い」と聞いたりすると、牛の糞の「匂い」しか連想できないのである。困ったものである。あの農学部の畑がなければ、もしかしたら私は量子力学を好きになっていたかもしれない。そして、量子力学を極めていたかもしれないのだ...簡単に言えば私は量子力学の授業では落ちこぼれてしまったわけだ。
ところで、昔の科学者達を考えると、「色」に関わらなかった人を探すほうが逆に難しいように思う。ニュートン、マクスウェル、ヤング、ヘルムホルツなどが代表的である。当たり前である。物理・化学に関わらず、「光」には関わらざるを得ない。当たり前である。さまざまな計測を行ったり、エネルギーを考えたりする上で光は最も重要なモノである。
そして、「色」というものは「光」の大きな性質の一つである。しかも、それは「科学者自身にとっても」目に見える性質である。目に見えるものを無視する科学者は少ないと思われるので、科学者が「色」に関わらないわけにはいかないのだ。
割に最近の科学者でも、意外な分野の人が「色そのもの」の研究をしていることがある。例えば、シュレディンガーなども色空間の提唱をしていたらしい。確かに、量子力学から色空間へはつながりを感じないこともないのではあるが、少し意外でもある。そのシュレディンガーが提唱した色空間がどのようなものであるのか、私は残念ながら知らないのだが、波動を深く研究していたシュレディンガーが提唱する色空間というのは非常に興味のあるところである。また、化学。物理学者であるダルトンは自らも色弱であるため、特にその辺りのことを研究し、報告している。
さて、そのダルトンをinfoseekで検索してみると、
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
もちろん、WEBページは会社の心(色弱と色空間 その2) - WEBページのカラーを考える 3 - (1999.08.10)で作成したTrueColorも同じような目的のために作成したものであるが、あれはあまりにも大雑把なモノだったので、作り直してみたいのである。なお、今回は画像のRGBとL、M、S錐体の反応の間の変換は
 |  |
そこで、こういったWEB上の画像を読み込んで、
でやったL,M,Sの各錐体の感度が低いときの色覚シミュレーションを行うソフトを作成してみた。ソフトはこれである。前回と同じく、Susieプラグインを用いて画像を読み込んでいるので、「Susieの部屋」などから、Susie本体・あるいはプラグインを入手する必要がある。また、手間を惜しんだためProxy対応にはしていない。さて、動作画面サンプルを以下に示す。初期状態では
- ダルトンレンズ (http://www2u.biglobe.ne.jp/~ohsaka/index2.html )
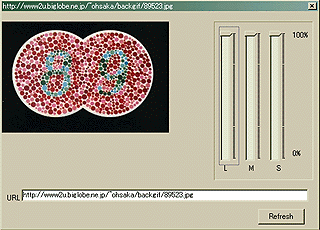 |
この画面例では各錐体の感度は全て100%になっている。
それでは、以下に適当に錐体の感度パラメータを変化させた場合のサンプルを示してみる。
 |  |
こうしてみると、これまで見てきたものとは違う数字が浮かび上がることがわかる。89,52などである。こういう仕組みを用いたのが、石原式などの色覚検査のやり方である。つまりは、異なる色を識別できないこと、すなわち、混同色を用いているのである。混同色を用いて文字を描くことにより、色弱であるかどうかを判断しようとするものだ。
さて、こういった書き方をすると、色を混同してしまうのが色弱の人だけと勘違いされてしまいそうであるが、そんなことはない。全ての人が「色を混同してしまう」のである。どんな人でも、異なる波長の光であっても、例えばRGBなどの(多くても)三色を混合すれば同じ色に見えてしまう。つまりは、混同色だらけなのである。健常者と呼ばれるヒトも色弱と呼ばれるヒトもたかだか数種類の錐体を持つにすぎない。
色々な光の波長分布を認識できる生物がいたとすると、彼らがからすればヒトは全て色弱ということになるのだろう。つまりは、五十歩百歩といったところなのかな、と思うのである。

