1998-12-27[n年前へ]
■Wveletで周期解析をしてみる 
音声・地震などの1次元信号や、画像等の2次元信号処理の解析というのはなかなか面白そうだ。そこで、周期ムラに対してWaveletをかけて周波数解析をする練習をやってみたい。また、短時間フーリエ変換とWaveletの比較もしてみたい。音声・地震などのデータはまた別にやってみることにして、今回は画像データを扱うことにする。ただし、いきなり2次元も何なので、画像データの周期(つまり1次元的な振動)に注目して、解析を行ってみたい。
まずは、「周期ムラのある画像」と「周期ムラのない画像」の2種類の画像を作成する。画像はいずれも数式を用いて作成した。X方向に変化する縞模様であり、表.1のような演算式になっている。一応、2次元画像ではあるが、Y方向にはなんの変化もない。2つの数式を見比べてみると判るが、いずれも2項からなり、低周波数のSinと高周波数のSinからなっている。「周波数ムラのある画像」では、その低周波数のSinの中にさらにSinがあるので、周波数がある周期で変化していることになる。一見、「周波数ムラのない画像」の方でも低周波数のSinの内部にさらにSinがあるように見えるが、0が掛けられているので、実際には存在しないのと同じである。
| 2つのSinからなり、その一方のSinの周期がムラ(一定の周期)をもっているもの。第二項目のSinの内部にさらにSinを入れることにより、周波数ムラを作っている。 | 2つのSin波からなり、どちらの周期も正確なもの。第二項目のSinの中のSinは0をかけてあるので、何ら影響を及ぼさない。 |
そのような数式に基づいて作成した画像を図.1に示す。なお縦軸がX軸であり、横軸がY軸である。図.2(b)では周波数ムラはないが、2つの周波数成分から作成されているため、うねりが生じている。
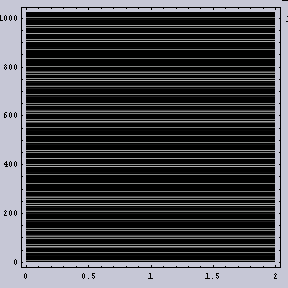 | 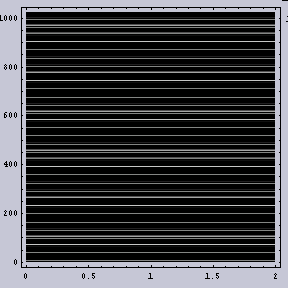 |
まずは、Wavelet変換である。図.2がその結果である。縦軸が周波数を示している。縦軸の上方向が高周波を示し、下方向が低周波を示している。また、横軸が原画像のX方向である。白は強度が小さいことを示し、黒は強度が強いことを示している。
いずれの画像も2つの周波数成分からなることが一目瞭然である。また、図.2(a):「周波数ムラのある画像」の方では低い周波数成分の方が、さらにある周期で周波数が変化していることがわかる。
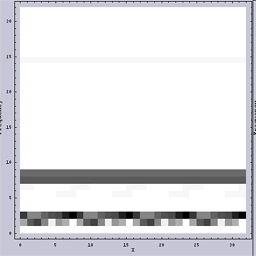 |  |
同じWavelet変換でも異なるFilterを用いてみると、結果は異なる。例えば、図.3がその例である。こちらの方が「周波数ムラ」がどのように生じているかを見るにはいいかもしれない。
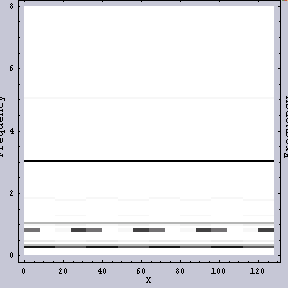 | 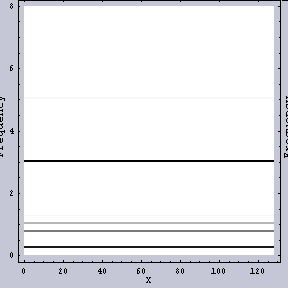 |
それでは、Wavelet変換ではなくて、フーリエ変換を用いて周波数解析を行ってみる。先ほどの1次元データの全領域に対してフーリエ変換をかけてみる。その結果が図.4である。ここで、横軸が周波数を示し、右側が高周波数を示し、左側が低周波数を示している。縦軸は強度である。
このフーリエ変換の場合も、2つの画像が2つの周波数成分からなり、図.4(a):「周波数ムラのある画像」では低周波数成分がぶれているのはわかる。しかし、その周波数ブレがどのようなものであるかまでは、わからない。
 |  |
なお、単純のためにウィンドー処理はしていない。そのために悪影響は当然出てしまう。
 |  |
単なる全領域にわたった周波数解析と、位置と周波数が同時にわかる解析の違いは非常に大きい。使いこなすのはなかなか難しそうだが....
1999-01-10[n年前へ]
■宇宙人はどこにいる? 
画像復元を勉強してみたい その1
知人から「自称UFO写真」というのものが冗談半分(いや100%位か)で送られてきた。その写真はボケボケの画像なので何がなんだかなんだかわからない。そこで、ぼけぼけ画像を復元する方法を勉強してみたい。UFOは冗談として、画像復元において進んでいるのは天文分野である。そこで、このようなタイトルなのである。もちろん、画像復元の問題は奥が深すぎるので、じっくりと時間をかけてみる。今回はMathematicaを使って試行錯誤を行った。
ボケ画像を復元するには、ボケ画像がどのように出来ているかを考えなければならない。そこで、ごく単純なぼけ画像を考えてみる。まずは以下の画像のような場合である。
 |  |
 |  |
画像:1のような点画像が、画像:2のような分布のボケ画像になるとすると、次のような関係が成り立つ。
(式:1) 画像:4 = 画像:3 * 画像:2
画像:1のような点画像が画像:2になるなら、それを参照すれば、画像:3のような点画像の集合がどう
ボケるかは計算できる。つまり、それが画像:4になる。ここで、*はコンボリューションを表している。
よくある信号処理の話で言えば、画像:2はインパルス応答である。といっても、これはごくごく単純な場合(線形シフトインバリアントとかいろいろ条件がある)の話である。まずはそういう簡単な場合から始めてみる。
このようなごく単純な場合には
(式:2) 画像:3 = 画像:4 * (1/画像:2)
とすれば、画像:3を復元できることになる。
そこで、まずは単純な1次元データで考える。下の画像:5のようにボケる場合を考える。ここでは、ガウス分布にボケるようにしてある。
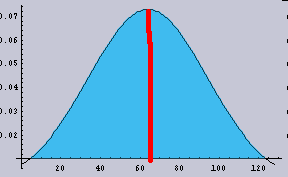 |
であったが、* すなわち、コンボリューションは
逆フーリエ変換(フーリエ変換(オリジナル画像) x フーリエ変換(ボケ具合))
と表すことができる。つまり、周波数領域で掛け算をすれば良いわけである。
 |  |
それでは、試しに適当な1次元データをつくって、画像:6とコンボリューションをとってやり、ボケさせてみる。
 |  |
逆フーリエ変換(フーリエ変換(画像:9) / フーリエ変換(画像:7))
= InverseFourier[Fourier[Image8] / Fourier[Image6]]; (*Mathematica*)
とやると、次のデータが得られる。
 |
(式:2) 画像:3 = 画像:4 * (1/画像:2)
を見るとわかるが、画像:2が周波数領域で0になる点があったりすると、計算することができない。また、0に近いとむやみな高周波数の増幅が行われて使えない。
そこで、この方法の修正として、ウィーナフィルターなどの最小平均自乗誤差フィルターがある。これにも多くの不自然な条件のもとに計算される(らしい)。しかし、infoseek辺りで探した限りでは、ウィーナフィルターを用いた画像復元の標準であるらしい。
この方法は先の逆変換に対して、次のように変形されたものである。Mathematicaの表記をそのまま貼り付けたのでわかりにくいかもしれない。
Noise ノイズのパワースペクトル
Signal 信号のパワースペクトル
Boke ボケる様子のインパルス応答
Conjugate 複素共役
BokeData ボケ画像
ResData1 計算した復元画像
Boke1 = (Boke^2 + Noise/Signal)/Conjugate[Boke]; (*Mathematica*)
ResData1 = InverseFourier[Fourier[BokeData] / Fourier[Boke1]]; (*Mathematica*)
である。Noise/SignalはS/N比の逆数であるから、SN比の大きいところではインバースフィルターに近づく。また、インバースフィルターの計算不能な点が消えている。
これを使って復元してみたのが、次のデータである。
 |
まずは、ボケのフィルター(PSF=PointSpreadFunction(どのようにボケるかを示すもの)、2次元のインパルス応答)である。
 |
 |  |
 |
その他線形の画像復元法をいくつか調べたが、ウィーナフィルターやインバースフィルターとほとんど同じような物が(素人目には)多かった。そこで、ウィーナフィルタなどとはやり方がかなり異なるものについて、いずれ挑戦してみたい。
関係はないが、ウィナーと言えばサイバネティクスが思い浮かんでしまう。当然、ロゲルギストが連想されるわけだが、文庫本か何かで岩波版と中公版の「物理の散歩道」が安く売り出されないのだろうか?売れると思うんだけど。新書版は高すぎる。
宇宙人はどこにいるか? そういった話は専門家に聞いて欲しい。わからないとは思うが。
さて、ここからは、1999.01.24に書いている。シンクロニシティとでも言うのか、今回の一週間後の1999.01.17に
日本テレビ系『特命リサーチ200X』で
地球外生命体は存在するのか?( http://www.ntv.co.jp/FERC/research/19990117/f0220.html )
という回があった。何とこの回のコメンテーターは先の専門家と同じなのだ。偶然とは面白いものだ。
2000-03-05[n年前へ]
■私の日本語練習帳 
アメンボ赤いなアイウエオ
もうすぐ、4月である。4月といえば、新学期だ。といっても、私は別に学生ではないので、新学期といっても特に何があるわけではない。別に新しい授業が始まるわけではないのである。しかし、私は何故かこの時期になると「英会話」を勉強したくなるのである。
去年の初めにも英語学習熱に襲われ、NHKのラジオ講座を通勤途中やることにしてみた。しかし、いつものように二ヶ月だけで挫折してしまった。そういうわけで、NHKラジオ「英会話」講座の毎年4月分のテキストが私の家には沢山ある。
それだけでなくて、この時期には「一週間でわかる英会話(仮名)」というような本も買い込んでしまう。しかし、これもまた買うだけで終わってしまっていたのだ。どうも、私の興味が散漫であることも理由の一つだろう。湯川秀樹は
「今日はあれをやり、明日はこれ、というように、あまり気が散ると、結局どれもものにならないですね。」という非常に的確なことを言っているらしいが、まさにその通りである。話題が飛びまくりの「できるかな?」には実に痛い指摘である。しかし、糸川英夫は
「自分にできること」よりも「世の中が求めていること」に挑戦し続けた方が人生も楽しい。と言っているらしいし、気にしないでおく(進歩無し)。
私はそういう生活が10年近く続いている。そんなわけで、英語のテキストは増えたが、英語能力は減る一方だ。いやまてよ、ということは
- 一人の人が持つNHKラジオ「英会話」講座の4月分テキストの冊数
- 一人の人が持つ英会話能力
- 今年のNHKラジオ「英会話」講座の4月分テキストを買わなければ、私の英語能力はアップする
いや、こんなワケのわからない仮説を論じている場合ではない。これは、非常にマズイ。今年こそ、三日坊主は止めなければならない。新しいミレニアムが訪れたことでもあるし、バージョンアップした私(仮に私2000とでも名付けておこう)になるためにも、今回こそ英会話の勉強をしてみたいと思う。
そこで、発売されてすぐ買ったは良いが、そのまま本棚で眠っていた
- BLUE BACKS 英語スピーキング科学的上達法 山田・足立・ATR人間情報通信研究所
- BLUE BACKS 英語リスニング科学的上達法 山田・足立・ATR人間情報通信研究所
それでは、今年の勉強を始めてみることにしたい。この本の主な内容は
- 英語における発音を科学的に分析(主にフォルマント、スペクトログラム)する。
これまで、「できるかな?」では
- 夜のバットマン - 超音波を可視化しよう- (2000.01.17)
- 着メロの音響工学 - この着信音は誰のだ!? 立体音感その3- (2000.01.08)
- 音場の定位を見てみたい - 立体音感を考える その2- (2000.01.03)
- 振動・声紋解析用のソフトをつくる-PCオシロソフトを高機能にしたい- (1999.01.07)
- オシロスコープソフトを作る- PCを2Ch高性能オシロスコープにしたい - (1999.01.03)
しかし、いきなり私に英語はキツイ。まずは日本語の練習から始めることにした。日本語の母音の発音を練習するのである。そうすれば、自分自身の日本語を再確認できるし、この本の信頼性もチェックできる。「フォルマントで音声を判断する」というのがどの程度使えるものであるかを、私の日本語でチェックすることができるのである。何しろ、変な発音かもしれないが、一応私は日本語のネイティブであるからだ。
それでは、「英語スピーキング科学的上達法」に付属のソフトで私のフォルマントを調べてみる。これが私の「あいうえお」のスペクトログラムとフォルマントである。
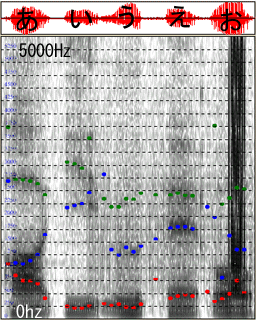 縦軸=周波数, 横軸=時間 |
ここで、色丸で示してあるのが
- 赤 = 第1フォルマント ( F1 )
- 青 = 第2フォルマント ( F2 )
- 緑 = 第3フォルマント ( F3 )
それでは、私の「あいうえお」をF1-F2空間にマッピングしたものを次に示す。これも、「英語スピーキング科学的上達法」に付属のソフトによるモノであり、標準的な男性の「あいうえお」の分布が示されている。そして、赤丸で示してあるのが私の「あいうえお」である。
そして、F1-F2空間における英語の母音分布の上に私の「あいうえお」を重ねたものも示す。
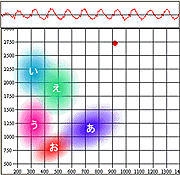 | 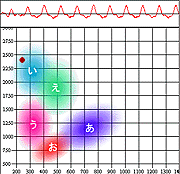 | 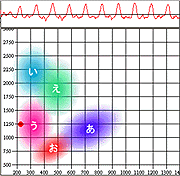 |
 | 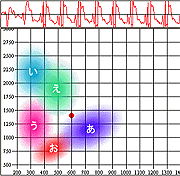 | 英語の母音に重ねてみた図 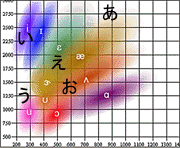 |
こうフォルマント分析をしてみると、私の「い」「う」「え」は標準的な分布の中に入っていることがわかる。しかし、「あ」「お」はそうではない。
むしろ、私は発音は英語の母音でいうところの
- 「あ」 =

- 「お」 =

- 私の発音の精度の問題 = 私の発音がヘン?
- 測定・解析の精度の問題
さて、最初のうちはこの本付属のソフトを使って遊んでいくことになると思う。しかし、いつか自作のソフトウェアを作成し、F1-F2-F3空間での「あいうえお」の可視化でもしてみたい。言葉の可視化、さらには言霊の可視化をしていく予定である。(あれっ、そう言えば英会話の勉強はどこへ…)
今日はあれをやり、明日はこれ、というように、あまり気が散ると、結局どれもものにならないですね。By 湯川秀樹
2000-03-12[n年前へ]
■元気な私とカゼひく私 
ガラガラ声の秘密
のどが痛いし、微熱がある。どうやら、扁桃腺が腫れているらしい。「あー」と言おうとすると、「あ”ー」という声になってしまう。まさにガラガラ声である。
ところで、ガラガラ声というのは一体どういう声なのだろう。もちろん、私の今の「あ”ー」という声はガラガラ声なのはわかる。しかし、このガラガラ声の特性をちゃんと定量化すべきだろう、と思うのである。まずは可能な限り、考えたり定量化したりしなければならないだろう。「感覚的なもの」というのは、そういうことをした後に持ち出すべきである。(考えること無しに)感覚的に判ったつもりになっているのは、何も感じていないのと同じである。それは、「想像力の欠如」に至ってしまうと思う。そして、想像力の欠如は「その人の地平線」を狭く(狭いという表現はおかしいようにも思うが)してしまう。何かワケの分からない文章だと感じるようであれば、それは私の頭が熱でふらふらになっているせいである。
さて、
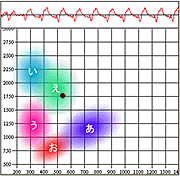
で私の「アイウエオ」の声についての解析を行った。今回も、同じように私の「アイウエオ」の声について調べてみたいと思う。そうすれば、過去の「元気な私」と現在の「カゼひく私」の声の違いがわかるかもしれない。そして、ガラガラ声とは一体何なのか?ということの手がかりが掴めるかもしれない。 まずは、前回と同じように - F1-F2空間における私の「アイウエオ」 - を調べてみる。カゼをひいてガラガラ声になることで、私の「アイウエオ」のフォルマントはどう変化しただろうか?次の図がF1-F2空間における「元気な私のアイウエオ(●)と扁桃腺が腫れている私のアイウエオ(●)」を示したものである。
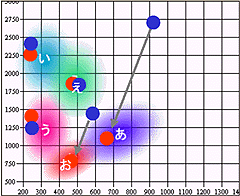 |
面白いことに、前回標準的な分布から外れていた私の「ア、オ」が今回は標準分布の中に収まっている。ガラガラ声になることで、私はやっと標準的な「アイウエオ」になるようである。何故だか、よくわからないが、面白い。まぁ、きっとフォルマント判断の際のピーク検出精度の問題だとは思うのであるが、不思議な結果である。
それでは、この「アイウエオ」の変化は一体どのようなものだろうか?音声波形を見てみることにする。それが次に示す図である。
まずは、「あ」の波形である。
元気な私  扁桃腺が腫れている私  |
元気な私の「あ」が割に単純な正弦波に近い。ただし、完全に上下対称な正弦波ではなくて、上に凸な部分の方が若干立ち上がりが速い波形のように見える。そして、割に綺麗に同じ波形が繰り返されている。
それに対して、扁桃腺が腫れている私の「あ」はスパイクノイズの入っている波形になってしまっている。こちらもスパイクノイズの入り方は割に同じ繰り返しである。
また、元気な頃の私の「あ」がF1-F2空間における標準的な「あ」分布と離れていたのは、F2が弱いせいではないかという予想ができるのではないだろうか?本来、上下の立ち上がりが異なるのが普通であるが、私の「あ」は上下が比較的同じであり、それでフォルマント判断の際のピーク検出精度が低下していたのではないか、という考えである。
それに対して、扁桃腺が腫れている私の「あ」は上下の立ち上がりがかなり異なり、周波数ピーク検出が容易であったのではないか、と私は考えるのである。
さて、次は「い」である。
元気な私  扁桃腺が腫れている私  |
これもやはり、基本的には同じ波形であることはわかる。しかし、元気な時には上に尖っている部分が、扁桃腺が腫れている私の「い」ではまるで部分的に上下逆転しているかのようになってしまっている。まるで、周波数毎の位相特性が異なっているアンプやスピーカーのようである。
次が「う」である。ここまでくると、同じ「う」に聞こえるのが不思議なくらいである。
元気な私  扁桃腺が腫れている私  |
見た目には、完全に別物の波形に見えてしまう。しかし、フォルマント上は「元気な私」と「扁桃腺が腫れている私」でほぼ同じ(F1-F2空間における私の「アイウエオ」を参照)であることを考えると、
- 各周波数の位相がずれている
- 高周波が重畳されている
次の「え」も「う」と同じ傾向である。フォルマント上は同じというのが、目で見る限りはよくわからない。いや、もしかしたら見慣れたらわかるようになるのかもしれないが、今の私の心の目ではよくわからないのである。
元気な私  扁桃腺が腫れている私 元気な私  |
最後の、「お」はもう何が何だかわからない。しいて言うならば、元気な私の「お」は高周波が極めて多いが、扁桃腺が腫れている私の「お」は高周波はあまりない。きっと、扁桃腺が腫れている私のノドの応答特性が低下しているせいだろう。しかし、これまでのスパイクノイズが増えている事実とどう繋がるかは、難しいところである。うーん、違うかもしれない…
元気な私  扁桃腺が腫れている私  |
ここまでは音声波形を見てきたが、最後に周波数空間での違いを示してみる。元気な私のアイウエオに比べて、扁桃腺が腫れている私のアイウエオは割に高周波が増えていることがわかる。やはり、先の「お」の考察は違っているのかもしれない。
 |  |
扁桃腺が腫れている私の声の周波数が高い辺りにいくつも見えるピークは私の「のどの痛みの証し」である。あ”ー、しんどい。いや、ホントにしんどいのである。
さて、私は鈴が鳴るような綺麗な声がとても好きなのである。いつか、そういう声の秘密について調べてみたい、と思うのであった。また、色々な歌手の声のスペクトログラムについても調べてみたい、と思う。
2000-04-09[n年前へ]
■心に浮かぶハートマーク 
色覚の時空間特性で遊んでみよう
4月である。「四月物語」の4月である。
で書いたように、私は4月だけは英語の勉強をしたくなるのである(何故なら、全然できないから)。そこで、ここのところ英語の先生のところに足繁く出向いている。その時に、信号機の例題を出されて「青信号」と言おうとして私は"ablue light"と言ってしまった。すると、「青信号は"green"だ -> The run signalis green.」と言われてしまった。しまった、確かにその通りだ。いや、英語でそう表現することに納得という話ではない。英語ではこうだと言われたら、私はそのまま頷くのみである。"Yes,sir"状態である。納得したのは、信号機の「現実の」色の話だ。そう言えば、日本でも信号機は「緑色」だった。試しに、信号機の一例を次に示してみる。 実は人にそう優しくないユーザーインターフェースの一例 |
本当は「緑色」なのに、「何故、青信号と言われていたのだっけ?」と考えながら、帰り道に交差点、「緑」信号をじっと見ていた。すると、「緑」信号は消えて、黄信号になった。しかし、私の目にはその瞬間「赤」信号が見えたのである。
私は夢を見ていたわけでも、予知能力があるわけでもむろんなくて、それは単なる錯覚である。「緑」信号が消えた瞬間に「赤」信号が見える、という錯覚である。
私が見た「赤」信号機の錯覚を実感してもらうために、こんなアニメーションGIFを作ってみた。ソフトをレジストしてないが故の、SGという文字は気にしないでもらいたい。下の画像中央にある黒い点を見つめていて欲しい。すると、緑のハートマークが消えた瞬間から、赤いハートマークがおぼろげに見えるはずである。
|
これは、色覚の時間特性による錯覚の一つである。実際に、赤いハートマークがあるわけではない。私の心の中にだけ、浮かぶハートマークである。
その原因となる色覚の時間特性を示すグラフを以下に挙げる。これは色覚の時間特性を示すグラフの例である。色覚のインパルス応答のようなものである。ある色を見た後には、その色の反対色を感じるということを示している。
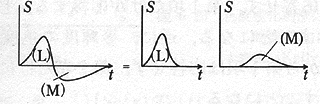 |
このような錯覚というのはとて興味深いものである。視覚という「デバイスの特性」が「目に見えて実感できる」ことが特に面白い。以前、
- 分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
- ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
さて、先の錯覚は色覚の時間特性によるものだった。それと全く同じような錯覚が、色覚の空間特性から得ることができる。そのような錯覚の一つにこのようなものである。それを下に示してみる。
 |
この有名な画像パターンを見れば、「白い線の交差部が赤く見える」はずだ。
これは、色覚の空間特性によるものである。これを示すグラフの例を以下に示す。この場合もやはり色覚の時間特性のように、ある刺激があるとその周囲に反対の色の影響が表れる。例えば、周りに白が多いと、その部分は黒っぽく見える。赤色の周りは緑がかって見えるのである。逆に緑色のものの周りは赤く見えるのだ。
そして、それをさらに進めると、周囲に赤色が少ない場所は、周りに比べて赤く見えるのである。上の画像で言えば、白の交差部は、赤の刺激が少ないので、赤の刺激を逆に感じるのである(ちょっと説明をはしょりすぎかな)。
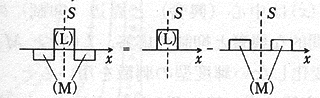 |
今回は、このような色覚の空間特性をシミュレートしてみたい。道具は単純にPhotoshopだ。もう手作業でやってみるのだ。ネコの色覚で遊んだ
の時と同じである。 | これがオリジナル画像。黒背景に白い線で格子模様が描かれている。 |
 | 白い(つまり光刺激が多い領域)からの影響を考える。先に示したグラフのように、光刺激がある箇所と少し離れたところではそれと逆の刺激を受けたような効果がある。 そこで、まずは白い部分からの影響をガウス形状のボカシにより、真似してみる。ある画素から少し離れた所に影響が及ぶのをシミュレートするのである。 |
 | 白い部分からの影響(実際には、比較問題となるので黒い部分からの影響と言っても良いだろうか?)は「白と逆の方向、すなわち黒い方向」に働く。 そこで、上の画像を階調反転させる。すなわち、ある画素から少し離れた所に元の明るさと逆の影響が及ぶことをシミュレートするのである。そしてさらに、階調のカーブを鋭くしてやる。 |
 | 上で計算したものとオリジナルの画像を加算してやる。これが、人間が感じる画像をシミュレートしたものである。 白い格子の交差点部が黒く見えているのがわかると思う。といっても、もともとその部分は黒く見えていたとは思うが。 下に、シミュレート画像とオリジナル画像を並べてみる。 |
 |  |
このようにして、オリジナル画像を見たときに感じる錯覚をシミュレートできたことになる(もどきだけど)。
さて、上では簡単のためにグレイスケールで遊んでみたが、最初に示した赤白の場合のようなカラーの例を示してみる。次に示す四角形の中央部は、右と左ではいずれも右の方が赤っぽく見えるはずである。緑に囲まれた領域は、本来の色に対して、緑と逆の赤色に見えるのである。上に示した白黒格子と全く同じ理屈である。
|
|
|
|
さて、この右下の画像中の赤は通常の「赤」よりもさらに鮮やかな「赤」を実現していることになる。左下のものと同じ赤100%の色であるが、左よりももっと鮮やかに見えている筈だ。右下と比べると、左下の赤は落ち着いた赤色に見えてしまうのではないだろうか?
この右下の赤、すなわち緑に囲まれた赤は、物理的にCRTあるいは液晶(今あなたがこのWEBページを見ているデバイス)などの表現可能領域を越えた、さらに鮮やかな赤色に見えているわけだ。ヒトの視覚のデバイス特性が故に鮮やかに見えることになる。
さて、鮮やかな「赤」と言えば、「ポケモンチェック」によれば、日本民間放送連盟のガイドラインには
- 映像や光の点滅は、原則として1秒間に3回を超える使用を避けるとともに、次の点に留意する。
- 「鮮やかな赤色」の点滅は慎重に扱う。
- 前項1の条件を満たした上で1秒間に3回を超える点滅が必要なときには、5回を限度とし、かつ、画面の輝度変化を20パーセント以下に押さえる。加えて、2秒を超える使用は行わない。
- コントラストの強い画面の反転や、画面の輝度変化が20パーセントを超える急激な場面転換は、原則として1秒間に3回を超えて使用しない。
- 規則的なパターン模様(縞模様、渦巻き模様、同心円模様など)が、画面の大部分を占めることも避ける。
しかし、その「赤」と「緑」パターンが細かくなると、何故だか不快なのだ。色覚の時空間特性を考えると、「赤」と「緑」の細かいパターンというのは、もしかしたら読む際に刺激が強すぎるのではないか、と想像してみたりする。根拠はたいしてないのだけれど。




