2001-01-27[n年前へ]
■オッパイ星人の力学 仏の手にも煩悩編 
時速60kmの風はおっぱいと同じ感触か?
本サイトhirax.netは「実験サイト」というジャンルに分類されることが多いようである。何が実験で、何が実験でないのかは私にはよくわからないのだが、とにかく「実験サイト」と呼ばれるサイトは数多くある。そして、その数ある実験サイトの中でも、人間そして愛について日夜取り組んでいるサイトの一つが「性と愛研究所」である。その「性と愛研究所」を読んでいると興味深いことが書いてあった。テレビ番組の「めちゃめちゃイケてる!」の中で何でも「時速60キロの風圧はおっぱいの感触である」と言っていたらしい。そしてまた、「性と愛研究所」では「おっぱいの感触と風圧に関する考察」の中で、「時速60kmでは全然おっぱいの感触ではなくて、ちょうど時速100kmを境に急におっぱいの感触を感じます。」というメールを紹介しながら、
「時速100kmの風では、本物は触れないけどお手軽に疑似体験、名付けて『プリンに醤油でウニ』ではなくなってしまう。それでは、まるで『キャビアにフォアグラでトリュフの味』だ。青少年のために疑似おっぱいを探してあげる必要があるな。」と結論づけている。
この「時速60kmの風」現象は「できるかな?」的にとても興味深いと思われるので、今回じっくりと考えてみることにしてみた。そして、この結論に何らかのプラスαをしてみたいと思う。
そう、前回「オッパイ星人の力学 第四回- バスト曲線方程式 編- (2001.01.13)」でオッパイの表面で働いている力について考えてみたのは、実は単に今回・そしてさらに次回の話のための準備だったのである。(さて、ちなみに今回は会話文体をメインに話が進む。「性と愛研究所」ではないが、この手の話は会話文体の方が書きやすいように思うし、私のバイブル「物理の散歩道」でも「困ったときの会話文体」と言われていたので挑戦してみた次第である。言うまでもないが、AもBも私が書いてはいるが、私自身ではない。)
A : 「東名高速で出勤途中に確認してみたんだが、やはり時速100kmあたりが妥当な感じだったな。」
B : 「何を根拠に妥当なのかがよくわからないが、確かに時速60kmでは手に何かが触っているという感触すらないな。それにしても、哀しい出勤の景色だぞ、それ。」A : 「ほっとけ!だけど、少し考えてみると、このおっぱい(ニセモノ)の感触問題は結構面白く、技術的にもなかなかに深い話だと思うんだよ。」
B : 「はぁそうですか…、としか言いようがないな。」A : 「まぁ、聞け。何しろこのおっぱい(ニセモノ)の感触問題には流体力学のエッセンスがぎっしりと詰まっているんだからな。」
B : 「そんな話は聞いたことはないが、とりあえず聞かせてもらおうか。」A : 「このおっぱい(ニセモノ)の感触問題を解くためには、とりあえず車の窓から手を出したときの指の周りの空気流を計算すれば良いわけだ。」
B : 「ちょっと待て。何で指の周りなんだ。手のひらじゃなくて?」A : 「簡単なことさ。試しにおっぱいを揉む仕草をしてみろよ。」
B : 「こ、こうか?あぁっ?手のひらじゃなくて指で揉んでるっ!」A : 「そうだろ。何故かわからないが、おっぱいを揉む仕草=Mr.マリックが超魔術をかける時のような指使いらしいんだよ。」
B : 「うむ、確かにそのようだな。」A : 「だから、時速60kmの風からおっぱいの感触を受けているのは指先だと考えるのが自然だろ。それなら、とりあえず下の図のような「指の間を抜けていく空気の流れ」を計算してみれば、おっぱい(ニセモノ)の感触問題が解けるわけだ。」
B : 「実写の手に二次元の計算結果を三次元的に合成するという凝った処理が、実にクダラナイことに使われている例だな…」
 | 高速で走る車の窓から手を出して、その手の指の間を抜けていく空気の流れを計算しよう。 鉛直方向の指の等方性を考えて、右の図に示すような指を輪切りにするような水平面のみを考える。 こんな写真を撮るときに、自己嫌悪に陥りがちなのは何故だか知りたい今日この頃。 |
A : 「こういう「空気の流れ」ような流体の力学は、ニュートンのプリンキピアに始まり、オイラーとベルヌーイにより非圧縮・非粘性の理想流体の運動方程式とエネルギー保存則が導かれた。それがオイラーの運動方程式とベルヌーイの式だ。オイラーの運動方程式はちなみにこんな感じだ。」
加速度 = 外力 + 圧力勾配力 v : 速度 |
A : 「基本的には「加速度 = 外力 + 圧力勾配力」という形だな。この非圧縮・非粘性の理想流体の場合はラプラシアンがゼロのポテンシャル流れと呼ばれる単純な流れになる。試しに、そんな場合をNast2Dを元にしたプログラムで計算してみた結果はこんな感じになる。ホントはこの計算自体は完全な理想流体ではないのだが、まぁ大体はこんな感じだ。」
B : 「おっ、あっという間に計算したな。」A : 「まぁ、ポテンシャル流れならエクセルでもちょちょいと計算できるくらいだからな。ちなみに、これは窓から手を出してしばらくしてからの空気の流れだ。」
 |
A : 「で、どうだ?」
B : 「いや、どうだ、と言われても困るが、なんかキレイだな。だけどちょっと小さくて見にくいなぁ。」A : 「そう言われれば確かにそうだ。じゃぁ拡大してみるか。」
 |
B : 「で、この結果から何がわかるんだ?」A : 「この図で空気は左から右へ流れているわけだが、左端の空気の速度と右端の空気の速度は、実は同じなんだ。」
B : 「そう言われても、よくわからないが?」A : 「指を通り過ぎてく空気は、指をとおる前後で運動量がそのまま変わってないってことさ。つまり、空気は指を通り過ぎる時になんら抵抗を受けてないってことだ。」
B : 「えっ?おかしいじゃないか、それなら逆に言えば指も空気から何の抵抗を受けないってことか?」A : 「そういうことだ。これがダランベールのパラドックスだ。」
B : 「じゃぁ、何か?この指先に感じるまぎれもないおっぱいの感触は幻だとでもいうのか!? そんなのオレは認めないぞ!」A : 「まぎれもない、っていうほどのものでもないし、ニセモノおっぱい自体は何か一種の幻のような気もするが、もちろん感触自体は幻であるハズはない。そもそも、空気をサラサラな理想流体として取り扱ったところが間違っているわけだ。そこで、登場するのがナヴィエとストークスだ。彼らはオイラーの運動方程式に粘性を導入した。全てはおっぱいの感触を説明するために、だ。」
B : 「それウソだろ。ナヴィエとストークスが聞いたら怒るぞ。」
加速度 = 外力 + 圧力勾配力 + 粘性力 v : 速度 |
A : 「見ればすぐわかるだろうが、この非圧縮流体に対するナヴィエ・ストークスの方程式は、最後に粘性項が入っている以外はオイラーの運動方程式と全く同じだ。」
B : 「なるほど。こうしてみると意外に簡単な式だな。」A : 「あぁ、オイラーの運動方程式に粘性項が入っただけだからな。そのせいで計算はちょっと複雑になるが、最近のパソコンならノープロブレムだ。というわけで、粘性を考慮して計算してみた結果が次の図だ。」
 |
B : 「おっ、ちょっと様子が違うな。何か、ジェットエンジンみたいに尾を引いてるぞ。」A : 「そうだろ。指の後ろのl様子がずいぶんと違うだろう。で、これを拡大してみたのが次の図だ。」
 |
B : 「左端の空気の速度はもちろんさっきと同じだが、指の後ろでは空気が渦巻いているし、右端の空気の速度は全然違うな。」A : 「もっとリアルに、窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみた計算結果のアニメーションが次の図だ。指の周りに空気が渦巻いていく様子がよくわかるハズだ。」
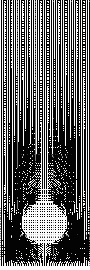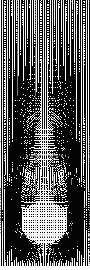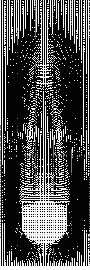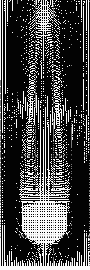 | 窓の外に手を出したときの、指の周りの空気の動きを時間を追って計算してみたもの。指の周りに空気が渦巻いていく様子がよくわかる。 メッシュを細かく切ったおかげで、計算結果は1GB弱。なんてこったい。 |
B : 「指が空気の中を走り抜いていく様子がよくわかるな。確かにこれなら、空気の抵抗を受けまくりだな。」A : 「そうだ。空気は指から力を受けるし、逆に、指は空気からしっかりと力を受けるわけだ。」
B : 「なるほど、この計算結果は指先に感じるまぎれもないおっぱいの感触を説明しているわけだな。いい感じじゃないか。流体力学そして粘性項さまさまじゃないか!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「おやっ?ちょっと待てよ!これでは、ただ現実を説明してみただけで、何の解決にもなってないぞ!時速60kmと時速100kmの風の感触の差を説明しているわけでもないし、青少年のためのもっと安全な擬似おっぱいを提供しているわけでもない!」A : 「いや、それがそういうわけでもない。実はこの先があるんだ。このナヴィエ・ストークスの方程式の解はレイノルズ数という無次元数によって決定されるんだ。今回の場合で言うと、レイノルズ数は「指の直径x 車の速度 / 流体の運動粘性率」という形になる。そして、このレイノルズ数が大きくなるほど渦が延びていくんだ。」
B : 「なるほど、わかってきたぞ。つまりあれだな。時速60kmから時速100kmに速度を上げれば、それに応じてレイノルズ数が大きくなって、空気の渦もおおきくなるし、おっぱいの感触も確実なものになるわけだな。勉強になるな。」A : 「う〜ん、実際には密度の違いの方が大きいんだが、ナヴィエ・ストークスの方程式の理解としてはそれでいいかもな。あと、単にレイノルズ数を大きくしたかったら指を太くする、っていうのでもいいわけだ。」
B : 「そう言われても指の太さはなかなか変えられないしなぁ。」A : 「指サックとか色々手はあると思うが、もっといい方法がある。さっきの式を眺めてみれば流体の運動粘性率が小さくなれば、レイノルズ数は大きくなる。例えば、水の運動粘性率は空気のそれの十五分の一だ。」
B : 「ってことは、水の中だったら、レイノルズ数も大きいし、密度も大きいし、指先に抵抗を受けまくりってことだな。すると、水中で手を動かしてみれば、それは空気中の高速クルージングと同じってことになるな!」A : 「そうさ、風呂の中で手をひとかきすれば良いだけの話さ。何もわざわざ時速100kmの車の窓から手を出す必要はないんだ。実際、風呂の中で確かめてみたけど、なかなかイイ感じだ!」
B : 「時速100kmで走る車の窓から手を出すのに較べれば、風呂の中で手をひとかきすれば良いだけなんて、まさに青少年のためのもっと安全な擬似おっぱいだな!」A : 「あぁ、それも全てナヴィエとストークスのおかげだ。」
B : 「それはもういいっ言ってるだろ。」A : 「ところで、ふと考えてみたことがあるんだ。さっき、指を太くすれば遅い速度でもレイノルズ数が大きくなるって言っただろ。東大寺の大仏なんかかなり指が太いじゃないか。」
B : 「確かに、そうだな。」
A : 「今調べてみると、大仏の掌の長さは256cmだ。つまり普通の人間の10倍くらいある。だったら、指の太さも10倍はあるだろう。ってことは、ほんのそよ風が吹いただけでも、大仏の手にはしっかりとしたおっぱいの感触が感じられているんじゃないのかな?」
B : 「単に手が大きいから空気の抵抗も大きいだけどいう気がしないでもないが、指の長さもでかいしさぞかし超巨乳の感触かもしれんな!そう考えると、あの大仏の手も何か実にイヤラシイ手つきに見えてくるから不思議だな!」A : 「う〜ん、悟りを開いているから、指先のヘンな感触なんかには惑わされないんだとは思うけどな。しかし、案外と仏もそんな煩悩と日夜闘っていたりするのかもしれないなぁ。しかも、その煩悩がホントーにあるのかもよくわからない幻のような擬似おっぱいってところが面白くないか?大仏の指先は二十一世紀の煩悩そのものを暗示しているのかもしれん。仏の手にも煩悩ってところだな!」
B : 「言いたい放題だな、全く。」
さて、今回は「オッパイ星人の力学第四回 - バスト曲線方程式 編- (2001.01.13)」と繋がるところまで話が辿り着かなかった。おっぱいの表面張力、マボロシのような指先の流体力学、そして大仏の煩悩をめぐる大河ドラマは人生そのもののようにまだまだ続くのである。
2001-07-31[n年前へ]
■水平線の彼方 
Over The Horizon
先日、富士の五合目から地平線を眺めていたのだけれど、そこで「水平線の向こうには何があるのだろう?」なんてことをふと頭に浮かべてしまった。「そこまでしか見通せない」という線が水平線なのだから、もちろん水平線の向こうに何があるのか見えるわけがない。だけど、だからこそ「その水平線の向こう」に何があるのかが、少しばかり気になってしまった。

そういえば、少し前に英和辞書を読んでいた時に、" on [over] the horizon"で「兆しが見えて,将来起こりそうで」を意味する、なんて書いてあった。「水平線の向こう、水平線の彼方」にある「何か」は「将来起こりそうな、何かの兆し」というわけだ。
あぁ、そうかぁ、と私は思わず納得してしまった。確かに、水平線の向こうに例えばもし何かの波があれば、それはきっといつか私たちの目に見えるようになって、そして私たちの足元にまで辿り付くことだろう。水平線の向こうにある波は止まることなく進み続けているのだから、例え水平線の向こうにあっても将来必ず私たちの場所まで辿り着くのである。
もちろん、水平線の向こうにある波を私たちが見通すことはできるわけはないのだけれど、だけどその気配を私たちはきっと感じるのだろうと私は思う。「水平線の彼方」にあるものは、「将来起こりそうな何かの兆し」であって、水平線の向こうにいるその気配には強い存在感があるはずだろう。
そんな「水平線の彼方にある波」を考えるとき、私はこんな話を思い出す。
地球はよく「水の惑星」と呼ばれる。確かに、そう呼ばれるくらいに地球には水が溢れている。何しろ、地球の表面積の七割が海なのだ。しかし、そうは言っても、地球の表面が全部水に覆われている、というわけではない。私たちが生活している陸地だって、「残りの三割だけ」とはいえちゃんと存在している。それなら、表面全部が水で覆われている「水の惑星」がもしもあったとしよう。そんな水の惑星のどこかで高い津波が生じたら、一体どうなるだろう?例えば、その水の惑星の南極である日突然津波が生じたとしよう。その時その津波はどんな風に伝わっていくだろう?
その津波の動いていく様子を図示してみたのが、下のアニメーションだ。
自分と正反対の場所で生じた波が自分の足元まで辿り付いて、生まれた場所と正反対の場所で生まれた時と同じ大きな津波になっているということを考えると、どうしても不思議な感覚に襲われる。そして、自分と正反対の場所で自分の足元で生じているのと同じ高波が生じている、ということもまたちょっと不思議だ。まるで、自分と正反対の場所に「もう一人の自分」がいるみたい、だ。「もう一人の自分」が、自分からは見えない水平線の向こうにいるなんてちょっと面白い感覚だ。
南極(図の下部)で発生した津波は進むに従って、段々と小さくなっていく。最初は南極の一点に集中していたエネルギーが段々と広がって拡散していくのだから、波が進んでいくにつれその高さはどんどん低くなる。そして、赤道を通過する頃には津波の高さはとても小さくなってしまう。ところが、その波が赤道を過ぎたとたんに津波は逆に強まりはじめる。赤道を通過した後は、津波の前方はだんだんと狭まっているので、こんどは津波のエネルギーが集まり始めるわけだ。それまでは、低くなる一方だった津波の高さは、今度は逆に徐々に高くなっていく。そして、ついに津波が北極に辿り着く時には、かつて南極で津波が発生したときの高さを再現してしまう。生まれた地点のちょうど反対側で、津波が生まれたときと全く同じ高波が発生するのである。
私たちの裏側で津波が発生したとしても、その津波は徐々に小さくなりながら進み続け、そして私たちの足元でその津波は再び大きな高波となるのである。そして、その津波はその後も同じように進み続けて、また南極で大きな高波となる。南極から発した高波がもう一度南極に集まってまた高波となるとも言うことができるかもしれないし、あるいはそれは、北極で集まった高波が南極で集まってもう一度同じ高波となる、とも言えるだろう。
そしてまた、「水平線の彼方にある波」はそれと似たこんな話も思い出させる。
宇宙の曲率が正で閉じた球状空間だった場合、私たちが発した光はどうなるだろう? 私たちからどんどん離れて行く光は空間の四方に広がって行くが、何時の間にかその光は徐々に近づき始める。そして、はるか彼方のある一点でその光が集まり、そしてまたその光は広がり始める…。そしてついには、その光は私たちのいる場所に集まり始める。私たちを取り囲む全ての方向から、かつて自分が発した光がやってくることになる。かつての自分があらゆる方向に見え出すのである。
水平線の彼方には何があるのだろう?水平線の向こうを見通すことは、私たちにはできないけれど、遥か彼方にいる波は「将来必ず私たちの足元に訪れる」。そして、もしかしたらそれは「かつての自分が発した波」かもしれないし、「どこか自分と正反対の場所にいる誰かが発した波」かもしれないし、それは廻り回ってやっぱり、「自分が発した波」なのかもしないし、やっぱりそれとも…なんて考えてしまったのである。
2001-08-31[n年前へ]
■後から?前から? 
「モンロー・ウォークのアニメーションGIF」。アップする前に仲野さんに相談。「一体、このアニメーションGIFはOKなのか自分でも考えちゃうんですよねぇ。アダルトサイト扱いされる今日この頃だし。」「いや、いいんじゃないの?前からの動画だったらマズイかもしれないけどさぁ。」「な・なるほど。前からの動画なんて発想はチットモありませんでした。そういう自分に一安心と言う気分です。ハイ。」
とはいえ、Poserだから前からの顔はちょっとコワイ。(リンク)
2002-09-01[n年前へ]
2002-10-03[n年前へ]
■洛陽の電脳ビル 
歩いていると(というより滑っていると)いくつも電脳ビルをみかけた。このビルは5階くらいだったか?下がハードで、最上階がソフト。ソフトCDは一枚50円くらい。ソフトは「PCアプリケーション・映画・テレビ・音楽」辺り。洋画全集(もちろん動画で)や日本のアニメーションや香港映画辺りを買うのであれば結構品揃えはあるかもしれない。特に、ちょっと古めというのであれば(新しいのが少ないような気がする分だけ)見つけやすいかもしれない。