2000-04-09[n年前へ]
■心に浮かぶハートマーク 
色覚の時空間特性で遊んでみよう
4月である。「四月物語」の4月である。
で書いたように、私は4月だけは英語の勉強をしたくなるのである(何故なら、全然できないから)。そこで、ここのところ英語の先生のところに足繁く出向いている。その時に、信号機の例題を出されて「青信号」と言おうとして私は"ablue light"と言ってしまった。すると、「青信号は"green"だ -> The run signalis green.」と言われてしまった。しまった、確かにその通りだ。いや、英語でそう表現することに納得という話ではない。英語ではこうだと言われたら、私はそのまま頷くのみである。"Yes,sir"状態である。納得したのは、信号機の「現実の」色の話だ。そう言えば、日本でも信号機は「緑色」だった。試しに、信号機の一例を次に示してみる。 実は人にそう優しくないユーザーインターフェースの一例 |
本当は「緑色」なのに、「何故、青信号と言われていたのだっけ?」と考えながら、帰り道に交差点、「緑」信号をじっと見ていた。すると、「緑」信号は消えて、黄信号になった。しかし、私の目にはその瞬間「赤」信号が見えたのである。
私は夢を見ていたわけでも、予知能力があるわけでもむろんなくて、それは単なる錯覚である。「緑」信号が消えた瞬間に「赤」信号が見える、という錯覚である。
私が見た「赤」信号機の錯覚を実感してもらうために、こんなアニメーションGIFを作ってみた。ソフトをレジストしてないが故の、SGという文字は気にしないでもらいたい。下の画像中央にある黒い点を見つめていて欲しい。すると、緑のハートマークが消えた瞬間から、赤いハートマークがおぼろげに見えるはずである。
|
これは、色覚の時間特性による錯覚の一つである。実際に、赤いハートマークがあるわけではない。私の心の中にだけ、浮かぶハートマークである。
その原因となる色覚の時間特性を示すグラフを以下に挙げる。これは色覚の時間特性を示すグラフの例である。色覚のインパルス応答のようなものである。ある色を見た後には、その色の反対色を感じるということを示している。
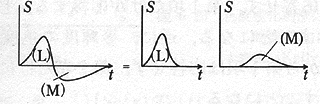 |
このような錯覚というのはとて興味深いものである。視覚という「デバイスの特性」が「目に見えて実感できる」ことが特に面白い。以前、
- 分数階微分に基づく画像特性を考えてみたい-同じ年齢でも大違い-(1999.02.28)
- コピー機と微分演算子-電子写真プロセスを分数階微分で解いてみよう-(1999.06.10)
- ゼロックス写真とセンチメンタルな写真- コピー機による画像表現について考える - (99.06.06)
さて、先の錯覚は色覚の時間特性によるものだった。それと全く同じような錯覚が、色覚の空間特性から得ることができる。そのような錯覚の一つにこのようなものである。それを下に示してみる。
 |
この有名な画像パターンを見れば、「白い線の交差部が赤く見える」はずだ。
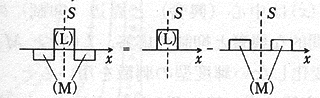
これは、色覚の空間特性によるものである。これを示すグラフの例を以下に示す。この場合もやはり色覚の時間特性のように、ある刺激があるとその周囲に反対の色の影響が表れる。例えば、周りに白が多いと、その部分は黒っぽく見える。赤色の周りは緑がかって見えるのである。逆に緑色のものの周りは赤く見えるのだ。
そして、それをさらに進めると、周囲に赤色が少ない場所は、周りに比べて赤く見えるのである。上の画像で言えば、白の交差部は、赤の刺激が少ないので、赤の刺激を逆に感じるのである(ちょっと説明をはしょりすぎかな)。
 |
今回は、このような色覚の空間特性をシミュレートしてみたい。道具は単純にPhotoshopだ。もう手作業でやってみるのだ。ネコの色覚で遊んだ
の時と同じである。 | これがオリジナル画像。黒背景に白い線で格子模様が描かれている。 |
 | 白い(つまり光刺激が多い領域)からの影響を考える。先に示したグラフのように、光刺激がある箇所と少し離れたところではそれと逆の刺激を受けたような効果がある。 そこで、まずは白い部分からの影響をガウス形状のボカシにより、真似してみる。ある画素から少し離れた所に影響が及ぶのをシミュレートするのである。 |
 | 白い部分からの影響(実際には、比較問題となるので黒い部分からの影響と言っても良いだろうか?)は「白と逆の方向、すなわち黒い方向」に働く。 そこで、上の画像を階調反転させる。すなわち、ある画素から少し離れた所に元の明るさと逆の影響が及ぶことをシミュレートするのである。そしてさらに、階調のカーブを鋭くしてやる。 |
 | 上で計算したものとオリジナルの画像を加算してやる。これが、人間が感じる画像をシミュレートしたものである。 白い格子の交差点部が黒く見えているのがわかると思う。といっても、もともとその部分は黒く見えていたとは思うが。 下に、シミュレート画像とオリジナル画像を並べてみる。 |
 |  |
このようにして、オリジナル画像を見たときに感じる錯覚をシミュレートできたことになる(もどきだけど)。
さて、上では簡単のためにグレイスケールで遊んでみたが、最初に示した赤白の場合のようなカラーの例を示してみる。次に示す四角形の中央部は、右と左ではいずれも右の方が赤っぽく見えるはずである。緑に囲まれた領域は、本来の色に対して、緑と逆の赤色に見えるのである。上に示した白黒格子と全く同じ理屈である。
|
|
|
|
さて、この右下の画像中の赤は通常の「赤」よりもさらに鮮やかな「赤」を実現していることになる。左下のものと同じ赤100%の色であるが、左よりももっと鮮やかに見えている筈だ。右下と比べると、左下の赤は落ち着いた赤色に見えてしまうのではないだろうか?
この右下の赤、すなわち緑に囲まれた赤は、物理的にCRTあるいは液晶(今あなたがこのWEBページを見ているデバイス)などの表現可能領域を越えた、さらに鮮やかな赤色に見えているわけだ。ヒトの視覚のデバイス特性が故に鮮やかに見えることになる。
さて、鮮やかな「赤」と言えば、「ポケモンチェック」によれば、日本民間放送連盟のガイドラインには
- 映像や光の点滅は、原則として1秒間に3回を超える使用を避けるとともに、次の点に留意する。
- 「鮮やかな赤色」の点滅は慎重に扱う。
- 前項1の条件を満たした上で1秒間に3回を超える点滅が必要なときには、5回を限度とし、かつ、画面の輝度変化を20パーセント以下に押さえる。加えて、2秒を超える使用は行わない。
- コントラストの強い画面の反転や、画面の輝度変化が20パーセントを超える急激な場面転換は、原則として1秒間に3回を超えて使用しない。
- 規則的なパターン模様(縞模様、渦巻き模様、同心円模様など)が、画面の大部分を占めることも避ける。
しかし、その「赤」と「緑」パターンが細かくなると、何故だか不快なのだ。色覚の時空間特性を考えると、「赤」と「緑」の細かいパターンというのは、もしかしたら読む際に刺激が強すぎるのではないか、と想像してみたりする。根拠はたいしてないのだけれど。
2000-04-24[n年前へ]
■ボクのテレビは白黒だった 
Benhamのコマを作ってみよう
「O plus E」のバックナンバーを眺めていると面白い記事があった。1985/7のNo.68に畑田豊彦氏が書かれている「生理光学 -各種運動知覚現象 -」である。視覚周りの色々な話が書かれていた連載である。なぜ、こういう記事を読んでいるかというと、少し前の、
で視覚特性の資料を探した時に、この畑田豊彦氏の連載を見つけて以来、どうもはまってしまっていたのである。 特に今回面白く感じたのはBenhamのコマ(Benham's top)である。Benhamのコマというのは次のような画像を「コマ」にして回転させるというものだ。次に示すのは、「Oplus E」に掲載されていた杉浦康平氏デザインのBenhamのコマである。
 |
このような画像を回転させると、白黒の模様しか描かれていないのに、何故かほのかに色づいた模様が見える。それが、Benhamのコマである。人間の視覚特性のために、白黒模様から色を感じてしまうのである。こういった「おもちゃ」で子供の頃に遊んでいたように思うのだが、すっかり忘れていた。きっと、理科の時間などにこういった「おもちゃ」で遊んでいたはずなのに、記憶の彼方に飛んでしまっていた。こういう記事を読み返さないと、たぶん忘れたままになってしまっていただろう。
ところで、プリンターをお持ちの方は、このWEBページを印刷して、コマを作成してみると面白いと思う。白黒プリンターで印刷しても、コマさえ作れば、アラ不思議、その回転するコマは色づいて見えるのである。モノクロプリンターでもカラー模様が印刷できるわけだ(人間が感じるところまで含めれば)。
他にも「O plus E」に掲載されていた杉浦康平氏デザインのBenhamのコマを示しておく。
 |
さて、このBenhamのコマを私も作成してみようと思う。もちろん、実際にコマは作成して楽しんでみたのだ。しかし、せっかくなので、動画ファイルの形で簡単に見ることができるようにしてみた。WEB上で簡単に見ることができるBenhamのコマである。
先の、「杉浦康平氏デザインのBenhamのコマ その1」を回転させるのではなく、時間的に変化する動画にしてみるのだ。といっても、こう書いただけでは判りにくいので、図で示してみる。まずは、作成した動画の各「コマ(このコマは静止画の意味)」を見てみよう。
 |  |  |
 |  |  |
これが、「杉浦康平氏デザインのBenhamのコマ その1」を時間的に変化する動画にしてみたものだ。この図で4,5,6コマめが、先のA,B, Cに対応しているわけである。
これをある程度高速で連続的に眺めると、この白黒模様が色づいて見えるはずである。まずは、これらの画像をアニメーションGIF画像にしたものを次に示す。とはいっても、作っては見たが再生スピードがどうにも遅い。これでは、色づいて見えるどころではない。このBenhamのコマをアニメーションGIFにする計画はひとまず挫折である。
 |
そこで、先の画像をAVIファイルにまとめたものを作ってみた。こちらの方ならスピードはなんとか満足できている(少なくとも、私の環境では)。AVIファイルということで、Windows以外の環境では不便だと思うが、動画変化ツールは色々あるから大丈夫だろう(多分)。
人によって、どの速さの場合が一番色づいて見えるかどうかは異なるだろうから、三種類の速度のものを作成してみた。それをここにおいておく。ちなみに、再生ソフトの設定を「自動繰り返し」にする必要がある。
さて、WEB上で情報を探してみると、面白い話があった。
- 色あそびコマ (http://www.avis.ne.jp/~g-k-toys/sakuhin.4.html )
昔、ウルトラマンをTVで見ていた頃、白黒TVで見ていた。その頃は、カラータイマーの色は私にはよく判らなかった。ボクのテレビは白黒だったからだ。ウルトラマンのカラータイマーの点滅をこのBenhamのコマのパターンで放送したりしたら、とても面白かったのにな、と思うのである。
2000-05-10[n年前へ]
■「モナ・リザ」の背景と自己相似性 
フラクタル地形を作ろう
以前、
で、「モナリザ」の微笑はどうにも奥深く見えるから不思議である。その微笑の先に何があるのかを深く考えさせる。そして、その答えはなかなか見つけられない。「モナリザの微笑」を眺め考えると、その先には結局「モナリザ」しか見えてこない。答えが見えないのであると書いた。そして、画像を読み込み、その画像をその画像自身の縮小画像(48x48個)で表現するjoconde.exeを作成し、自己相似形の「モナ・リザ」を描いてみた。それが、この下のjunhirabayashi 作 48x48の「モナリザ」である。
 |
ところで、本家のダ・ビンチの「モナ・リザ」と言えば、本当に奇妙な背景である。荒涼として、とても普通の景色とは思えない。地学の教科書に出てきそうな地形だ。グランド・キャニオンのような侵食地形のようである。
 |
ダ・ビンチは治水に関して深く興味を持ち、大好きだったと聞く(いや、もちろん本当に聞いたわけじゃないけれど)。ダ・ビンチは治水に関してはプロフェッショナルだった。それを考えれば、この「モナ・リザ」の荒涼たる背景なども、ダ・ビンチの趣味そのままのようで面白く感じられる。しかし、見れば見るほどこの背景は不思議である。Bryce等の「自然っぽい地形」を描いてくれるソフトで作成した景色のようである。
その手のソフトは想像上の地形を作成するのに大抵フラクタルを用いる。つまり、フラクタル地形である。フラクタル地形というのは、例えば山脈の一部分を拡大してみてもそこにはやはりその山脈自身と同じような高低があるということである。どんなに拡大してみてもそこにはやはり小さな山脈があるのだ。というよりは、どんなに拡大してみても、小さな山あり谷ありと言った方が良いだろうか。そういう自己相似性を利用してやれば「自然っぽい地形」を描けるわけだ。
「モナ・リザ」の微笑の中はどこまで拡大しても「モナ・リザ」の微笑がある、つまり「モナ・リザ」の前景は感覚としてのフラクタル性を持っているように感じられる。そして、背景もまたフラクタル性を顕著に持つフラクタル地形っぽいのである。ダ・ビンチが自己相似性、フラクタルについて考えていたと想像してみると、とても面白いと思う。
さて、フラクタル地形の説明を少しだけ書いたが、やはりここは自分でもそのフラクタル地形を作成してみなければマズイだろう。何しろ、私はフラクタル地形のことは良く知らない。とりあえず、自分で作成してみないことにはよくわからない。まずは実践あるのみだ(もちろん、トンデモナイ内容を実践するのは問題外だ)。
そこで、まずは手っ取り早くMathematicaでフラクタル地形を作成してみた。次のアニメーションGIF画像はMathematicaでフラクタル地形を作成していく様子である。荒いスケールの凹凸を作成して、その後段段と細かいスケールの凹凸を作成していくようにしてみた。プログラム時間は10分である。ここらへんの手軽さがMathematicaのスゴイ所だ。
 |
この計算は適当に作ってみただけなので色々と問題がある。例えば原点(0,0)から放射状に凹凸がある。これは計算上の問題である。しかし、今回は面倒なので深追いはしない(カッコつけて言う内容じゃないが…)。これを手直ししようとするととたんに面倒になってしまうのである。
とりあえず、完成したフラクタル地形は次のようになる。hirax山脈とでも名づけておこう。
 |
なかなか「自然な山脈」っぽくないだろうか?青い光に照らされた幻想的な山脈である。といっても、色がなんとも自然でなくて、「自然な山脈」には見えないという人も多いだろう。というわけで、色調を変えて、それっぽくしてみた。そこで、次が先の完成画像の色調を変えて、「自然っぽく」したフラクタル地形である。
 |
これが、Mathematicaで作成した「山岳地形」だ。結構、それっぽく見えると思う。今回は、Mathematicaの内部でレンダリングしたそのままであるが、次回(といっても、いつになるかわからないのはいつものこと)には、Mathematicaで作成した「山岳地形」を元にきちんとレンダリングしてみたいと思う。さぞや、幻想的な景色が作成できるに違いない。
さて、私はフラクタル図形を眺めているとなぜだか知らないが、水戸黄門の主題歌が頭の中で響いてくるのである。あの、「人生楽ありゃ苦もあるさ…」というヤツである。もう、流れ出したら止まらないのだ。それはもう水戸黄門の主題歌のフラクタルである。
そして、ひどい時には「どんぐりころころ」と水戸黄門の主題歌の輪唱が頭の中で始まってしまったりするのだ。それを「カノン」と言えば聞こえは良いが、いやもうホントにたまらない状態である。
どんぐりころころ、どんぐりこ人生楽ありゃ、苦もあるさお池にはまって、さぁ大変くじけりゃ、誰かが先に行く…
あぁ、止めてくれぇ…
2000-10-19[n年前へ]
■Evey little thing we ee is magic. 
WEBページで作るOscylinderscope
先日、The Reuben H. FleetScience Centerという科学館に遊びに行った。そこで面白いものをみかけた。それはOscylinderScopeという名前のもので、下の写真のようなものだった。
 |
Oscylinderscopeの作者のNorman TuckのWEBサイト
- A Catalog of Kinetic Sculpture byNorman Tuck
- ( http://www.normantuck.com/ )
- TheOscylinderScope
- ( http://www.normantuck.com/catalogPages/oscylinderScope.html)
電気的な変化する信号に合わせて、光の点をsweepさせることで波形を描き出すのがオシロスコープだが、このOscylinderScopeもドラムをい回転させて、ドラム上に描かれた白い線が振動するギターの弦の後ろをsweepして、ギターの弦の振動する様子を描き出すのである。
参考までにNorman TuckがOscylinderScopeに関して取得しているUnites StatesPatent 5,975,911から判りやすそうな図を下に示しておく。揺れる棒の様子がSin波状に見えている、という説明図である。
 | 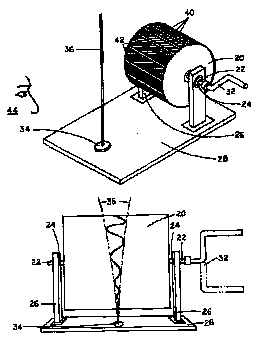 |
このOscylinderScopeにはとっても単純だけど素敵な科学的なアイデアと、展示物としてのセンスと、そして何故かちょっとうれしくなるようなバカバカしさが感じられて私はとっても大好きだ。そこで、一ファンとして私も「WEBページで作るOscylinderscope」というのをやってみることにした。
といっても、やることは単純に単なる速く移動する白い線をパソコン画面に映し出すだけである。そして、その前で何かを振動させてその振動の様子を可視化するのである。
まずは、Oscylinderscope風アニメーションGIFだ。おそらくInternetExplorerではゆっくりとしか再生されないと思うが、NetscapeCommunicatorであればプラットホームにもよるが高速に再生することができると思う。少なくとも、Linux上のNetscapeNavigatorではかなり速く再生されるハズだ。
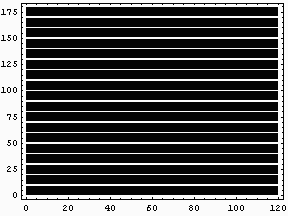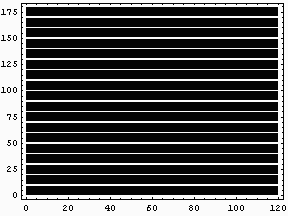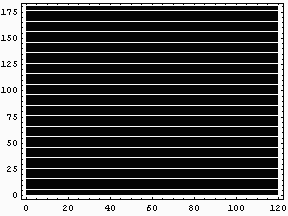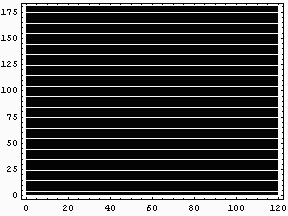 |
このアニメーションを再生できない環境の人のために、動画ファイル版にしたものもここにおいておく。
- oscylinderscope.avi ( 145kB )
このアニメーションGIFや動画ファイルを再生して、部屋の電気を暗くしてみる。すると、CRTの画面というのはとても明るいので、部屋を暗くしてCRTだけをつけておくと、CRT画面に映し出されている色に部屋が染まる。部屋がそんな風にチカチカした状態で、画面の前で何かを振動させると、アラ不思議その物体の振動の様子が何やら変な風に見えてくる。例えば、真っ直ぐな細い棒を「Oscylinderscope風AVIファイルの前で棒を揺らしてみたところ」である。写真では判りにくいと思うが、真っ直ぐな棒がウニョロウニョロと曲がって見えるだろう。とにかく、真っ直ぐな棒が振動する様子を静止したイメージで目にすることができるのだ。
 |
ところで、私はこんなOscylinderscopeを見ていると、ナポレオンズの「首グルグル・マジック」を連想してしまう。一カ所だけ穴の開いた筒を頭にかぶる。そして、穴の部分から顔を覗かせる。筒を回転させ始めると、なんと顔がずっと見え続ける、つまりエクソシストの少女のように首が回転しているのだ!これがマジックかぁ?と言う人も多いかもしれないが、私はこれこそ本当にmagicそのものだと思う。このマジックには、目に見えていない瞬間に起きていることは結局想像するしかない、という本当の真実と、何故かもう嬉しくなるくらいのバカバカししさが同居していて私は大好きなのだ。他の人はどう思うか知らないけれど。




