1999-08-08[n年前へ]
■瞳の中の真実 
目の屈折率を調べよう
先日、近所の海へ行ってきた。水中メガネで覗いているとまるで熱帯魚みたいな魚が泳いでいて素敵なのだ。水中メガネを使うか使わないかで、海の楽しさは雲泥の差である。水中メガネで覗いてみると、裸眼の時とは別世界のようにくっきり見えるのである。
 |
さて、「水中視の光学」と言えば、物理の散歩道の「アユと泳ぐ」(新物理の散歩道-第2集- 中央公論社)に詳しく面白い考察がされている。本WEBでもScrapsにて「焦点」ということを考えたばかりなので、「アユと泳ぐ」と同様の解析を「できるかな?」風に行ってみたい。光学シミュレーターを作ってみたいのである。そのために、まずは人間の目の中の屈折率を調べなければならないだろう。というわけで、今回は下調べ編である。
それでは、人間の左目の水平方向の断面図を調べてみる。
 |
この中で普通のカメラでいうレンズの役割を果たしているのはどこだろうか。レンズの部分を赤く塗るとどのようになるだろうか?下に並べた3つのうちどれだと思われるだろうか。
A | B | C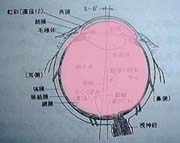 |
まずは、目の中の物質の屈折率を調べてみると、以下のようになる。
| 場所 | 屈折率 |
| 角膜 | 1.376 |
| 眼房 | 1.336 |
| 水晶体 | 1.386 |
| 硝子体 | 1.336 |
空気(15℃の乾燥空気)の屈折率はほぼ1.0であるから、空気と比較するならば、目の中の物質はほぼ同じ屈折率を持つといっても良い。角膜も眼房も水晶体も硝子体も同じ屈折率を持つとして良いだろう。すなわち、大雑把な近似においては図.2のCに示したようなピンク色のレンズがあるとして良い。つまり、目全体がレンズであり、レンズ面に焦点を結ぶようになっているのである。水晶体は若干の補正を行うに過ぎない。レンズの焦点はレンズから離れた場所にあるはずと思っている人もいるかもしれないが、レンズの表面に焦点があるものも実はよく使われている。
さて、人間が水の中に入るとどうなるだろうか?水は1.333(589.3nmの波長の光に対して)の屈折率を持つ。これは人間の目の中の物質の屈折率とほぼ同じである。水を主体として出来ている人間なのだからこれは当然だろう。しかしこれでは、目は光を屈折させることはほとんどできなくなる。そのため、水の中に入るときには水中メガネなどで目の回りを空気で満たしてやることが必要なのである。
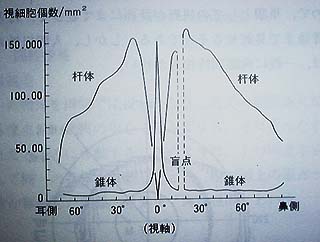
本題からははずれるが、資料を眺めていると、面白いグラフが目に入ってきた。人間の目の断面方向の視細胞個数の分布を示したものであり、錐体と桿体を個別に示してある。「盲点」なんかも図中にある。
 |
目に映る明るさって何ですか? - 君は天然色 - (1999.07.05)
の回に錐体と桿体については触れたが、桿体は1lx程度の暗さから働き、明るさのみに反応する。一方、錐体は10lx以上で働く。従って暗いものを見るには桿体の働きが重要になるわけだが、上のグラフは桿体が視点の中心にはほとんど存在していないことを示している。
従って、暗い所でものを見る際には、視点の中心では感度が足りなくなりやすいことがわかる。これまで、暗い星を眺めるときに視界の中心で見ようとすると見えないのだが、少し視点をずらしてやると見えるような気がしていたのだが、それは気のせいでは無かったようである。
さてさて、資料集めも終わったので「瞳シミュレーションソフトウェア」の開発に着手したいと思う。もちろん、時間がかかるのはいつものことだ。すぐにはできないけどね。
1999-11-27[n年前へ]
■The Way We Were 
君の行く道

CasioのE-500で撮影した写真である。道が不思議に輝いていた。
Michael J. Foxの出世作でもある"FamilyTies"というTVシリーズがある。日本語に訳せば、「家族の絆」というタイトルの通り、ある家族を中心としたコメディ番組だ。MichaelJ. Fox演じる長男、を含む家族達の周りの色々な話しが描かれている。コメディの珠玉の名品だと思う。
その「ファミリータイズ」の中で"The Way We Were"という話があった。日本放映時(ビデオ化)のタイトルは「キートン家の語り部おばさん」だったと思う。
ローズおばさんは、キートン一家の母方のおばさんだ。その母方のドネリー家の歴史をいつも話してくれる、キートン家の人気者だ。しかし、何かローズおばさんの様子がおかしい。そうしている内に、キートン家の家族達は、おばさんがアルツハイマー病にかかっていたことを知る。そのキートン家の長男でもあるMichael J. Foxは、現在パーキンソン病を克服しようとしている。
そして、アルツハイマー病を克服しようと決意したローズおばさんは、長女マロリーに、「お願いがあるの。私がこれまで話していた物語を、これからはあなたが伝えていって欲しい。」と頼む。そして、ローズおばさんの前でマロリーは長い長いドネリー家の歴史を語り始める。「時は1741年、冷酷なイギリスの統治によりアイルランドを暗雲が覆った... 」家族が集まる中、マロリーが最後まで語り終わると、ローズおばさんは黙って頷く。
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
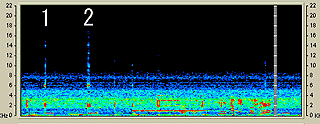 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-06-21[n年前へ]
2001-07-19[n年前へ]
■世界の果てにある「溶けないアイスクリーム」 
何処かでちょっと切なげなリフレインが聞こえた。聞き取れたのは「きっといつか溶けてなくなるアイスクリーム…」というところだけ。
だけど、世界の何処かにはきっとあるはず、と思ったらやっぱりあった。ぶらり旅の行く先はトルコにしようかな。「雲ひとつ無い青い空、不思議な景色、そしてアイスクリーム」だけを見に行くのも良いかも。(リンク)(リンク)