2001-03-04[n年前へ]
■柿ピーのシーソー・ゲーム 
柿とピーナツの供給バランスを考える
結婚しようとするカップルが少しばかり気にした方がよいのが、「柿ピーの好み」である。知らない人がいるとは思えないが、念のために書いておこう。柿ピーと言えば、柿ピー= 柿の種 + ピーナッツであって、亀田製菓の大ヒット商品である。そして、何と言ってもビールの安上がりのおつまみだ。
 |
この「安上がりで手軽なおつまみ」というところが、結婚しようとするカップルにはとても重要である。何故なら、結婚する前のカップルであれば洒落た店で飲むことも多いかもしれないが、結婚後はなかなかそうはいかない。いつの間にか手に持ったワイングラスは缶ビール(しかも発泡酒)に変〜身し、「テーブルの上の豪華な食事」はちゃぶ台の上の亀田製菓の柿ピーにバケラッタしているのである。
そうなると、かつては「このソースとても美味しいよね。うふっ。」なんて言っていた二人も変わらざるをえない。そりゃそうだ。柿ピーを目の前にして、気取ってみてもしょうがないわけだ。そんな時、こんな会話に走りがちである。
「柿の種ばっか、食べないでよ!」そう、柿ピーがなまじ「柿の種 + ピーナッツ」なので、片方がどんどん減っていったりすると、これがもう大変。かつては、ワインを片手に愛を語らっていた二人も、今やビール(しかも実は発泡酒)を片手に食い物の奪い合いをすることになるのである。
「オマエこそ、ピーナッツどんどん食えよ!」
これが、カップルの二人がとても似たもの同士で、「私達二人とも柿の種がスゴ〜ク好きだから、ピーナッツなんかいらないの。だから、- 柿の種だけが100%入った柿の種 - を買うの!」なんて感じなら、もちろんノープロブレムだろうし、あるいは、「ぼくらは、ピーナッツだけを買うのさ!」という感じのカップルでも同様だろう。
 |
あるいは、もう「ぼくは柿の種が好きだけど、きみはピーナッツが好き。二人は違っているから良い組み合わせなのさ。柿の種はぼくがどんどん食べるから、君はピーナッツをお食べ」なんてカップルでもいいだろう。こちらも、「ひとまずは」ノープロブレムである。つまりは、全く同じが正反対のカップルであれば、大抵の場合ほとんど問題はないのである。
しかし、「柿ピーは柿の種とピーナッツが適当な割合で入っているから良いのさ」なんていうグルメ気取りのカップルがいたりすると、大変である。
「アンタの食べる割合、少しおかしくない?」となるのは必至である。この数分後には、巨人の星の一徹父ちゃんのごとく、ちゃぶ台はひっくり返されているのに違いないのである。柿ピーの割合恐るべしだ。
「何言ってんだよ!オマエの方が柿ピー食べ過ぎだってんだよ!」
「そんなことないわよ!」
そして、しかもこれが理系カップルともなれば、もう最低だ。
「柿とピーの割合は7:3で食べなさいよ!」という具合になるに決まっているのだ。このままいくと、柿ピーを前にして離婚談義にもなりかねない。なんともオソロシイ話である。(* ピー柿は7:3でピーナツの方が多い。そんなのが実在することが私にとっては驚きである。)
「違うだろ、6:4が適正値に決まってるだろ!」
「そんなにピーナッツを食べたいなら、柿ピーじゃなくてピー柿*にしなさいよ!」
「別にピーナッツが過半数を超えるほどがイイって言ってんじゃねぇ〜!」
「何よ、もっと定量的に話しなさいよ!」
そういうわけで、「柿ピーの好み」「柿ピーの割合」「柿ピーの消費の割合」なんていうものは、結構結婚しようとするカップルには重要なのである。結婚しようとするカップルはぜひとも心して聞いておいてもらいたい。とはいえ、モテモテ度テストで
「女にモテない、というより、女に興味がないオマエ。今、一番気になることがドリキャスの値下げだったりなんかしない? まーそれも人生だけど、モテたほうがおいしいことは多いぜ? もうちょい女に関心持てよ。」と判定された私が言っても説得力がないか。
ところで、そもそも柿ピーの割合はどのくらいが普通なのだろうか?WEBで検索してみると、柿ピー10に対して
- 柿の種 : 7〜6
- ピーナッツ : 3〜4
そこで、試しに私も手元にあった小袋入り亀田の柿ピーの中身を調べてみた。調べたのは「小袋入り亀田の柿ピー」である。
 |
この一袋の中身を開けてみると大体こんな感じである。
 |
もちろん、単に数えても良いわけではあるが、「クダラナイことに、無意味なほどに大ゲサな道具を使うのがこのサイトのポリシー」でもあったりするので、まずは画像処理ソフトを使って柿の種とピーナッツの個数をカウントしてみた。使ったソフトはUTHSCSAImageTool である。PCベースでフリーでお手軽で粒子カウントとなるとこのソフトになるだろう。もちろんNIH-imageベースのScionImagePCという選択肢もないわけではないが、こと粒子カウントになるとはるかにImageToolの方が使いやすい。マクロの取っつきやすさ(機能は較べものにならないほどおちるが)もNIH-image系よりも上である。
さて、まずは上の画面内で柿の種を粒子カウントしてみたのが次の画面だ。この画面では見つかった柿の種は赤い縁取りがされ、個数がマーキングされていることがわかると思う。ちなみに、この画面内では93個の柿の種が見つかった。しつこいようだが、「数えた方が早いだろっ!」というツッコミはこの「できるかな?」では厳禁である。
 |
同じようにして、ピーナッツをカウントしてみたのが次の画面である。この画面では、ピーナッツは23個見つかった。
 |
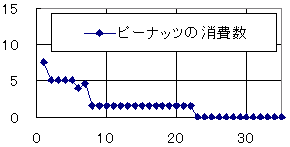
すると、個数ベースでピーナッツが23/(93+23) = 20%で、残りが柿の種で80%ということになる。柿ピーの割合は大体8:2であったことになる。確か、WEBの亀田製菓に関する情報では
「柿ピー」のブレンドは、柿の種6に対してピーナッツ4が基本と書いてあったような気がするので、今回の8:2というデータは測定誤差、とその他の何らかの誤差が重なったものだろう。いや、そんな誤差はどうでも良いか。
ところで、大きな袋に入った柿ピーを食べながらよく考えることがある。私は柿の種が大好きなので、柿の種ばっかり選んで食べていくと、袋の口近くの上の方にはピーナッツばかりが残り、明らかに袋の場所ごとに柿の種とピーナッツの割合が異なってしまっていることがよくある。この柿の種とピーナッツの割合の時間的・空間的変化は一体どうなっているものだろうか?そこで、今回その「ピーナッツの柿ピーに占める割合の時間・空間的変化」について、少し考えてみることにした。
まずは簡単に判るように、袋の中から均等に柿の種とピーナッツを「柿ピーの割合を適当な割合で」食べていった場合、「ピーナッツの柿ピーに占める割合」は次の図のようになる。この図は横軸が時間で、縦軸がピーナッツの柿ピーに占める割合である。
緑 : 柿ピーを8:3の割合で食べた場合  |
今回の場合柿ピーは8:2で入っているので、青の場合のように柿ピーを8:2の割合で食べていくと、時間にして10分後に柿ピーがなくなるまで、ピーナッツの柿ピーに占める割合は20%をキープしたままである。しかし、(少しばかりピーナッツが好きな人が)柿ピーを8:3の割合で食べてしまうと、つまりピーナッツを過剰に食べてしまうと、どんどんピーナッツの割合は減ってしまい、ついに8分経過後にはピーナッツが袋の中から無くなってしまうのである。つまり、あとの2分は悲しみと共に柿の種を食べ続けなければならないのである(私は柿の種が好きなので悲しくもなんともないが)。
じゃぁ、袋の中の空間的分布も考えてみたらどうなるか、というのを次に計算してみた。まずは、袋を大きく二つに分けて、袋の入り口で適当な割合で柿ピーを食べた後、袋の奥から袋の入り口の方へ柿ピーを持ってくる。また、その際に適度に柿ピーをかき混ぜる。そして、柿ピーがなくなるまで柿ピーの割合の変化を調べてみるのである。ちなみに、IE4以降+Excel2000以降?の人であれば、ここをクリックすれば、その計算シートで遊ぶことができると思う。
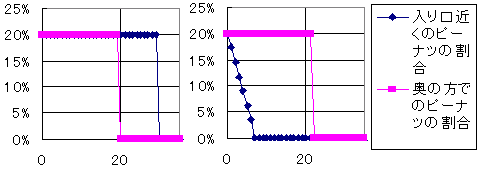
例えば、「柿ピーを8:2の割合で食べた場合」と「柿ピーを8:5の割合で食べた場合」のピーナッツの柿ピーに占める割合の時間・空間的変化を調べてみたのが、次に示す結果である。ちなみに、このいずれも横軸は時間である。また、時間軸にして30前後の時点で柿ピーは完全になくなっている。
 ちょっと計算上の誤差が大きいが、それはちょっと無視してもらいたい。 |
さて、左の「柿ピーを8:2の割合で食べた場合」、つまり本来の柿ピー比と同じ割合で食べていった場合には、入り口近くでも奥の方でも柿ピーの比率は変わらない。そして、入り口の方から柿ピーを取った分を、奥の方から補給しているので、奥の方では時間軸20の時点で空になってしまっている。左の図でピーナツの割合がゼロになっているように見えるのは、実は単に柿ピーがなくなっただけなのである。そして、入り口近くの柿ピーが時間軸30の時点で空になっているまで、柿ピーの比率は変わることはない。当たり前だ。
では、「柿ピーを8:5の割合で食べた場合」はどうだろうか?つまり、本来の割合よりもピーナッツを多く食べがちな人の場合だ。そんな場合の右を見てみると、奥の方は単に入り口近くに柿ピーを補給しているだけなので、柿ピーの割合は変わらないままだ。しかし、入り口近くではあっという間にピーナッツの割合が減ってしまっている。ほとんどなくなっている、といっても良いくらいの状態である。つまり、ピーナッツ大好き人間にとっては、手の届く袋の入り口近くには全然ピーナッツがないという、拷問状態なのである。周りに女子校や共学の学校はあるけど、自分の通う学校が男子校だったみたいなキツイ状態である。ちなみに、私は高校時代に私服の共学の学校に通った結果、制服の女子高生に強い強い憧れを抱くに至ったことを否定できなかったりするのである。
話を戻して、それでは「袋を適当にかき混ぜながら」、「柿ピーを8:5の割合で食べた場合」はどうなるだろうか?というのが次の結果である。こうすると、奥の方のピーナッツもどんどん消費されているのがわかる。入り口近くも奥の方も、同じようにどんどんピーナッツの割合がどんどん減ってしまい、時間軸15の時点で完全になくなってしまっている。あとは柿の種がなくなる時間軸30の時点まではもう柿の種と向かい合うだけの人生なのである。ツラすぎる(ピーナッツ好きの人にとっては)。私の知人のオッパイ星人が結婚後に妻から、
*一部、不適当な発言がありましたことをお詫びします。
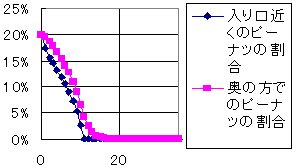 |
つまりは、ピーナッツが食べたいからといって、あまり柿ピーの袋をかき混ぜるのは良くないということなのである。もちろん、短期的にはピーナッツがたくさん食べることができて良いわけであるが、長期的に見ればその後の長い「柿の種人生」が待っているのである。それが端的にわかるのが、次の「ピーナッツをどれだけ食べているか」を示す結果である。
この結果の中で、上の方に示した「柿ピーの袋をかき混ぜない場合」では、結構最後までピーナッツを細々と食べていけることがわかるだろう。柿ピーがなくなるのが時間軸で30前後の時点であるが、その少し前23位の時点までピーナッツを食べていけるのである。それに対して、ピーナッツを早く食べたいばかりに、柿ピーの袋をかき混ぜまくりの下の「柿ピーの袋をかき混ぜた場合」には、時間軸で13前後の時点でもうピーナッツがなくなってしまっている。もう、コイツには「柿の種人生」しか残されていないのである。
| 柿ピーの袋をかき混ぜない場合
結構最後までピーナッツを細々と食べていける |
| 柿ピーの袋をかき混ぜた場合
なんとも、太く短くのピーナッツの食べ方である… |
とはいえ、柿ピーの袋をかき混ぜながら太く短くピーナッツを食べるか、それをじっとガマンの子で細々と最後までピーナッツを食べるか、どっちが良いかは難しいところだ。ちなみに、私はかき混ぜまくりで柿の種を食いまくり、残ったピーナッツは人にプレゼントするというとても良い性格である。だったら、100%柿の種を買えって感じであるが、売店には置いてないことも多いから、しょうがないのである。
というわけで、今回はビール(やっぱりあくまで発泡酒)を左手にそして柿ピーを右手でつまみながら、酔っぱらった頭で(いつものことだが)、ツマラナイことを考えてみた。モノが本当の柿の種であればオチて芽が出るのが普通なのだけれど、今回の柿ピーの話はオチがあるわけでも芽が出るわけでもない。酔っぱらいのタワゴトだから意味なんか全然ないのである。と、日記には書いておこう(意味不明)。
2001-10-16[n年前へ]
■ディズニーランドえとせとら 
と、色のことを書くとちょっと堅苦しかったので、ディズニーランド好きなあなたにこんな「今日のトクする一言」をプレゼントっと。
色々サンプル画像というものがあるわけですけれど、ディズニーランドのシンデレラ城を背景にした風景写真というのも多いです。何故かと言うと、ディズニーランドはシンデレラ城の色とかに非常に気を使ってます。つまりは、ディズニーランドの中の特徴的な建物の色管理がは非常にきちんとされているわけです。
だから、色を気にするサンプル画像の風景写真としては非常に良い被写体なわけです。数年後にも同じ色の建物がちゃんと品質保証された上で存在しているわけですから。
そこらへんが、かつて使っていた向が丘遊園とは違うというわけですね。向が丘遊園じゃペンキの色は退色してどんどん変化しちゃいそうだし。いや、それ以前にそれ自体がなくなっちゃうし。
2001-12-24[n年前へ]
■サンタが街にやってくる 
複数サンタクロースの巡回問題
簡易に書き直した2011年版もあります。
幼い頃、クリスマスの夜を清里の聖ルカ教会で過ごしたことがある。今では、「アイスクリーム」で有名になってしまった聖ルカ診療所の隣の教会だ。清里を通る小海線が蒸気機関車からディーゼル列車に切り替わった頃だった。私の住んでいた野辺山から一番近い病院がその聖ルカ診療所だった。今はどうなのか判らないけれど、あの病院の中の風景はまるで高原の療養所のようで(高原の診療所なのだから大して違いはないのだけれど)、とても不思議だった。
さて、クリスマスの人気者と言えば、やはりサンタクロースである。世界中の子供達から待ち焦がれられ、プレゼントを配って歩くのだから、クリスマスイヴのサンタは大忙しなのである。一体、サンタクロースはどんな風にプレゼントを配って歩くのだろう、と思った私は「サンタクロースの巡回問題」について考察をしてみることにした。
知らない人のために書いておくと、「巡回サンタクロース問題(TSP:TravelingSanta Problem)」というのは「巡回セールスマン問題(TSP:Traveling SalesmanProblem)」の特殊例である。そもそも「巡回セールスマン問題」というのは「n人の顧客の場所が与えられたとき、全ての顧客を一回ずつ経由して巡回する際に、移動距離が最小になる経路を求める。」という問題である。計算幾何分野で最もメジャーな話であって、カーマーカー特許などこれに関係するものである。つまりは、色々なものを配達する際には「配達経路を考えるのは実は結構大変なのだ」という問題なのである。
これまで「巡回サンタクロース問題」を考えた人がいなかったか、と言うとそんなことはなくて、試しにinfoseekで"サンタ"AND"巡回"で検索すると、既に素晴らしい研究がなされている。それが
- サンタクロース研究
- ( http://www.geocities.co.jp/HeartLand-Suzuran/5872/santa.html )
そこで、そんなこれまでの「巡回サンタクロース問題」に関する研究を踏まえながら、「できるかな?」ではさらに「サンタクロース巡回問題」を考え、そして、できることであればサンタの隠された真実にさらに迫ってみようと思う。「サンタクロース巡回問題」の中には、サンタクロースの真実に近づく鍵が含まれている、と私は何故か感じるのである。
まず、始めに問題提起をしてみよう。
「果たしてサンタは一人なのか?」
どのような事件においても(別に事件ではないが)、単独犯か複数犯かというのはとても重要な問題である。犯人が単独犯か複数犯かで証拠の指し示す意味は異なってくる。サンタは一人、と私たちは何故か思い込んでいるが、そんな先入観は正しい捜査のたまには捨てる必要がある。
そこで、まずはサンタの歴史から調べてみると、Santaさんの起源、クリスマスページ!によれば、サンタクロースの起源であるSt.Nicolausは西暦4世紀頃の人であるという。その頃の人口は現在よりもはるかに少なかった。それは、サンタの労働量がはるかに少なかったということだ。なるほど、この時代であれば、サンタは一人でも不思議ではないかもしれない。
とはいえ、Santaさんの起源の中の色々なサンタの目撃情報を見ると、本当にサンタは一人なのか疑問を感じるのもまた確かである。色々なサンタが目撃されている、ということはサンタは実は複数犯の可能性が高いのではないだろうか?
また、世界の人口は人口増加に示されている全世界の人口増加の様子を見れば明らかなように爆発的に増えている。ちなみに、そこに示されているグラフを対数軸にし、近似式を加えたものが以下である。
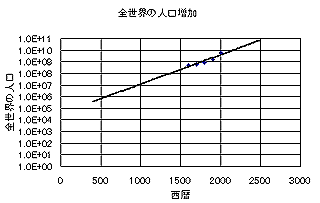 |
St.Nicolausのいた西暦4世紀頃に比べて現在の人口は4桁、すなわち、10000倍に増えている(近似式によれば。ホントのところは知らない)。これでは、サンタクロースは年々仕事量が驚異的に増えていることを意味する。もし、サンタが単独犯であるとするならば、過労死はまぬがれそうにない。
サンタの単独犯説に対する疑問は「サンタクロース巡回問題」からも示される。N人の顧客(今回の例ではN人の良い子供)が与えられたとき、サンタが計算しなければならない経路の総数は(N-1)!/2で与えられる。2で割っているのは「対称巡回サンタクロース問題(A家からB家間での距離と、B家からA家間での距離が同じという性質がある場合)」であるからだ。
子供の家N=100までの場合の、サンタが計算しなければならない経路の総数(N-1)!/2を以下に示してみる。
 |
どうだろうか、Nが少し増えると爆発的にサンタが計算しなければならない経路の総数(N-1)!/2が増えていくのがわかると思う。一軒多くなるだけで、ものスゴイ数の計算をしなければならなくなるのである。サンタが実際に配達して回るのも大変だが、その前に配達経路を決める計算量は実はもっと大変なのである。
先の人口増加の割合をこれに加えるならば、「サンタが計算しなければならない経路の総数」は天文学的数字になることは明白である。
そこで、私はやはりサンタ複数犯説が真実に近いと思うのである。サンタ複数犯説が正しいとするならば、ッ実はこの「サンタクロース巡回問題」は遥かに容易に解くことができるようになるのである。
それでは、複数サンタがいるときの「サンタクロース巡回問題」を考えてみよう。サンタが複数のm人いる場合を考える≠ニA「サンタが計算しなければならない経路の総数」はm*(N/m-1)!/2で示される。
一例として、サンタが1,2,10人の場合を示してみる。
 |
このグラフからサンタが複数いる場合と、単独の場合とで巡回経路を考える手間が全然違うのがわかるだろう。サンタが2人いると、計算量は半分になるのではなく、ものすごく少なくなるのである。
実際の巡回においての仕事量は、サンタがm人いれば1/mになる。しかし、その前準備はサンタがm人いれば((N-1)!/2)/(m*(N/m-1)!/2)分の一になるのだ。簡単に言えば、メチャクチャ楽になるのだ。サンタが一人では事実上サンタがプレゼントを配ることは不可能だけれど、複数犯であれば容易にプレゼントを配ることができるのだ。
このように「複数サンタクロース巡回問題」を考えることにより、サンタは複数いることが明らかだと私は思うのだ。
ただこれだけでは、不十分だ。全世界の子供達も年を経るに従って、爆発的に増えている。サンタが複数いるにしても、それでもやはり大変だ。サンタ達の人数も爆発的に増えていかなければ、とてもじゃないがやってられないことだろう。
それを解決する一つの答えはこうだ。「子供が増える割合に従って、サンタも増える」と考えるのだ。子供が一人増えると、サンタも一人増えるのだ。そうすれば、何の問題もない。子供が一人現れると、サンタも一人増えるのであれば何の問題もなくなる。
ところで、「子供が一人現れると、サンタも一人増え、サンタの数が子供と同じ比率で増えていく」ということは、子供たちがいずれサンタになるという考えが自然だとは思えないだろうか。そうだ、子供達がサンタになるのだ。子供達が大人になって、そしてサンタになるのだ。
もしかしたら、それはサンタという名前ではないのかもしれない。普段は他の名前で呼ばれているのかもしれない。けれど、クリスマスだけはサンタという名前になるのだ。電話ボックスで着替えるちょっと情けないスーパーマンのように、クリスマスイヴだけは彼らは変身するのだ。
こうして、サンタ達は子供の枕元にやってくる。むかし子供だったサンタ達が子供達の枕元にやってくる。そして、夢を見ている子供達が起きてしまわないように、そっと枕もとにプレゼントを置く。
サンタなんかこれまで私の枕元には来なかった、という人たちも多いのかもしれない。けれど、きっと、そんな人たちもまたサンタになっていくのだろう、そして、その時、本当にサンタがいる、ということに気づくのだろう。
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
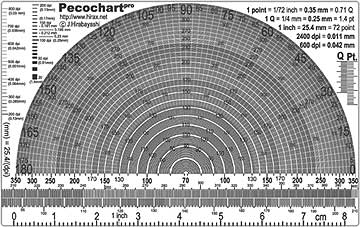 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。
2002-12-03[n年前へ]
■クリスマスツリー 
夜のエスカレーターホールの一番上にあるクリスマスツリー。金色のクリスマスプレゼントを指にとってみたり、銀の玉の向こうの世界を眺めてみたり。そんなことをしてる内にどうやらシャボン玉が降ってきたらしい。