1998-11-29[n年前へ]
■鴨川カップルの謎 
そうだ、京都、行こう
京都の風物詩の一つに「鴨川カップル」がある。京都を流れる鴨川の川縁に、カップルが等間隔に並ぶ現象である。鴨川の三条大橋から四条大橋までがその舞台である。この鴨川カップルについては、いくつかの性質が知られている。
- 基本的にはカップルらは等間隔に座る。
- 暗くなるに従い、カップル間の間隔が狭まる。
- 電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる。
- 夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。
- 夏はカップル数が多く、冬は少ない。
- 男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない。
 (四条大橋の上から撮影) |
 |
 |
(この後、1999.05.04午前中に撮影した画像も示す。午前でもあるにも関わらず、上の時より密度が高い。もちろん、夜の密度の高さはこんなものではない)
 |
今回の目的は、「鴨川カップル」のこのような性質はなぜ生じ、そこに効いているパラメータを実測することである。
まず、性質2,3(暗くなるに従い、カップル間の間隔が狭まる、電灯の近く、すなわち、比較的明るいところではカップル間の間隔は広がる)より、明るいと隣のカップルと離れようとする力が大きくなると予想される。また、カップル同士が離れようとする力、斥力、のバランスにより性質1(基本的にカップルらは等間隔に座る)が形成されていると考えられる。
性質3(夏はカップルの間隔が狭まり、冬はカップルの間隔が広がる。)の季節による間隔の違いは性質4のカップル数の違いから来ているのかもしれないし、それ以外の何らかのパラメータがあるのかもしれない。性質4(夏はカップル数が多く、冬は少ない)はやはり「寒さ」のせいであろう。京都は本当に寒い。いくらアツアツのカップルとは言えども、寒いものは寒い(多分、想像だが)。当然、建物の中でのデートとなるだろう。自ずと、鴨川カップルは少なくなる。
性質5(男性が連れ立って、しかも何人かで座っていると、その周りにはカップルはなかなか座らない)については、「男性の群れ」というのは普通のカップルに比べて非常に強い斥力が働いていると考えられる。この性質5に関しては、私の実体験を持って語ることができる。私と友人連中が鴨川の川岸に近づくと、座っている鴨川カップルが離れていく、という経験を何度もしたことがある。やはり、強い斥力が働くのだ。
計算は全てMathematica3.0を使った。計算の例をMathematicaのNotebookで示す。また、計算の考え方を以下に示す。
 | 鴨川の川縁を真上から見た所。画面上部が鴨川。画面下部が歩道。画面中央に街灯がある。そのため、画面中央が一番明るい。 |
 | カップル達はこの辺りに座る。 |
 | 対称性を考えて、画面の左半分のみを考える。また、赤い線上にカップルが座るものとする。 |
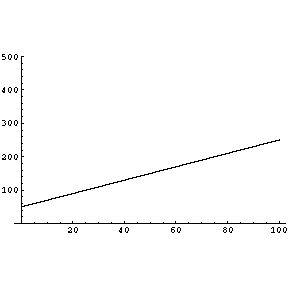 | その線上の明るさを模したもの。X=100の所が街灯の直下とする。 このような明かりに照らされた状態で、カップルが照らされているとする。 |
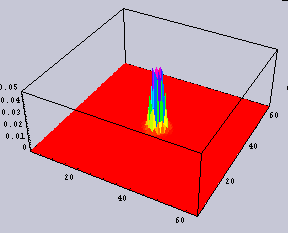
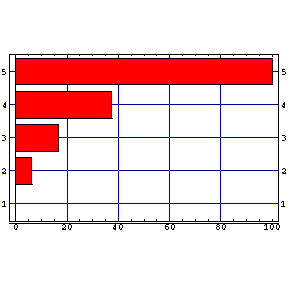 | 100m内にカップルが5組として方程式を解くとこうなる。棒グラフの先端の位置がカップルの座っている位置を示している。1組目は0m地点、5組目は100m地点、すなわち、街灯の直下である。 明るい所ではカップルの間隔が離れているのが判ると思う。 カップルの居心地(隣のカップルの存在感=隣のカップルの明るさ/距離)はいずれも、8という値である。カップルの居心地指数は少ないほど快適であることを示す。 |
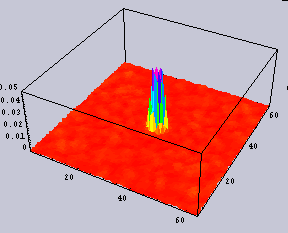
それでは、条件を振ってやってみたい。上からだんだん暗くなっていく。鴨川の半日である。また、カップル数はいずれも100m辺り5カップルである。
 |  | 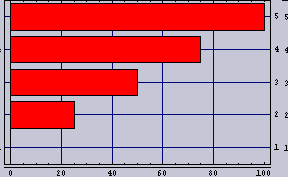 | 20 |
 |  | 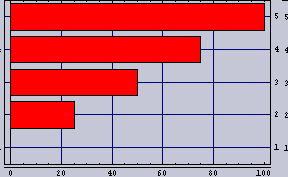 | 16 |
 |  | 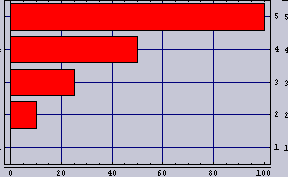 | 10 |
 |  | 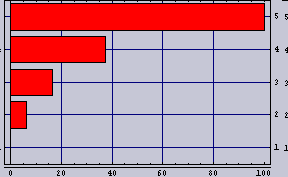 | 8 |
 |  | 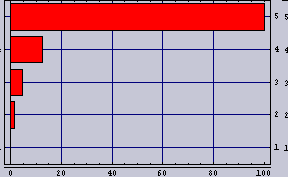 | 6.4 |
昼間はカップルが等間隔であり、夕方になり、街灯で照度分布ができると、カップルの間隔も分布ができている。といっても、そういう条件で解いているのだから、当たり前だが。
また、カップルの居心地は暗くなった夜の方が快適であるのがわかると思う。それは、カップルの様子を見ていても、その通りであると思う。しかし、快適であるからといって、カップルが何をやってもいいという意味ではない。そこは、はっきりしておきたい。
今回は、カップル数を全て同じにしたが、逆に同じ居心地指数であるという条件下で解けば、夜の方がカップルが多いという性質も再現できる。これらの計算モデルと実験を比較していくことにより、鴨川カップルの性質を実証していくことができるだろう。なお、今回は計算の簡単のため、男性連れの効果は組み入れていない。また、いつかもう少しまともな計算をしてみたい。
計算を行った感想だが、実に不毛な計算であった。気が向けば、モンテカルロシミュレーションによる鴨川カップルの検証も行いたい、と思う。が、気が向く日はきっと来ない。
1999-02-25[n年前へ]
■微小4次元計測をしてみたい 
デジタルカメラ、実体顕微鏡、動画の三題話
最近はデジタルカメラ(以降、デジカメと呼ぶ)が大流行りである。実験の記録に使うと大変便利だ。ところで、実体顕微鏡の接眼部からデジカメで撮影するという話題が
の辺りにある。この撮影法の難しさは、デジカメの種類によって違う。例えば、FujiFilmのFinePix700では光軸合わせに結構苦労する。ところが、ソニーの「DigitalMavica(技術者向けのオプション(例えばオシロスコープ・フード)などもあって便利)」ではこの撮影方法はとても簡単である。「Mavica」のレンズを実体顕微鏡の接眼部に合わせるだけで、視野をうまく合わせることができる。といっても、実体顕微鏡にはCCDなどを接続してあることが多いため、単に実体顕微鏡の接眼部をデジカメで撮影するだけでは面白味が少ない。もちろん、高いCCDカメラの代りにメガピクセルのデジカメを使えるメリットは大きいとは思う。
しかし、実体顕微鏡(双眼式)で何が良いかといえば、立体に見えることである。しかし、CCDカメラの接続は一眼式になってしまう。これまで、一つの実体顕微鏡に2つのCCDを接続できるような実体顕微鏡は見たことがない。そこで、接眼部からデジカメ撮影をする方法なら、立体撮影をすることができるので、実体顕微鏡の長所を生かすことができる。
これがそのサンプルである。交差法と平行法の両方を示す。立体に見えるはずである。
 |  |
 |  |
それでは、3次元計測を行ってみる。まずは、マーキングをする。基板上とICチップ上にA,B,C,Dという4つのマーキングを行う。
 |  |
奥行き方向(Z方向としておく)に違いがある場合には、左右の画像でX方向のずれが生じる。そのずれ量を計算してやれば、Z方向の計測を行うことができる。つまり3次元計測を行うことができる。
| 左 | X | Y | 右 | X | Y |
| A | 124 | 33 | A | 133 | 35 |
| B | 13 | 55 | B | 22 | 55 |
| C | 136 | 167 | C | 144 | 167 |
| D | 101 | 100 | D | 99 | 102 |
左右画像の(x,y)の差をとり視差を出す。すると、(A,B,C)とDの間で違いが有り、Z方向の距離が違うのがわかる。
| 左-右 | X | Y |
| A | -9 | -2 |
| B | -9 | 0 |
| C | -8 | 0 |
| D | 2 | -2 |
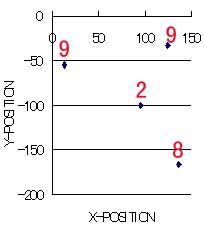
この結果から、(x,y,z)を描くと以下のようになる。x-y座標上にzの値を書いてある。Dのポイントのみがz方向に近いのがわかる。
 |
もちろん、本来は光学系から係数などを導くのだが、今回は行っていない。大雑把な説明である。また、同じようなやり方で、3次元表面計測も行うことができる。
ソニーの「DigitalMavica」の素晴らしい所は光軸合わせが簡単なだけではない。動画をmpegファイルとして撮影することができる。というわけで、2台買えば実体顕微鏡の画面を立体動画として保存できる。それが微小四次元計測である。
残念ながら、今回は1台しか使えないので、動画サンプルを示すだけである。mpegファイルをgifに変換したものを以下に載せておく。TFT液晶の拡大画面である。映像の終わりで実体顕微鏡の接眼部からカメラを外しているのがわかると思う。
動画サンプル MPEG形式 507kB
動画サンプル GIF形式155kB (上を縮小したもの)
その他関連情報
1999-02-27[n年前へ]
■画像ノイズ解析について考える 
考える理由
画像ノイズ解析を目的として、2次元フーリエ変換を用いて周波数解析をすることが多い。かねがね、このやり方について疑問を感じていたので少し考えてみたい。その疑問とは次のようなことである。
- 通常の2D-FTでは、入力データ全領域での周波数解析を行う。従って、単発のパルスのようなノイズはバックグラウンドに埋もれてしまい、結果にはなかなか出てこない。
- 同じ理由で、2D-FTでは位置と周波数解析を同時に行うことができない。(もちろん、短時間フーリエ関数を使えば、そのような測定は行うことができる。)
- また、ホワイトノイズのようなフラットな周波数特性を持つノイズもバックグラウンドを押し上げるだけの効果しか持たないため、解析をしづらい。
2D-FTと2D-Waveletの例
はじめに、2D-FTと2DWaveletの例を挙げる。まずは2D-FTである。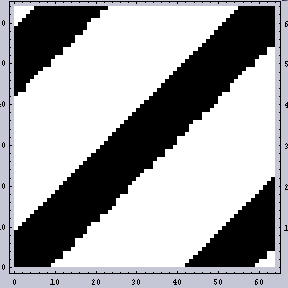 | 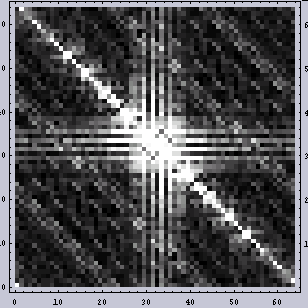 |  |
このように、2D-FTの結果というのは周波数(X,Y両方向)と振幅がわかる。ここでのスクリーン角のような周期性を持つものの解析にはフーリエ解析というのは極めて有効である。店で見かけるインクジェットプリンターもヘッドの移動による周期ムラが激しいが、このようなムラに対してフーリエ変換を用いた周波数解析を行うのは正当であり、有効だろう。
それでは、同じ画像に2D-Waveletをかけてみる。2D-Waveletの結果は位置と周波数強度分布情報(ホントは違うのだが)が両方出てくる。位置情報が2次元で周波数強度分布情報が1次元であるから、合わせて3次元である。そのため、表示に一工夫いる。
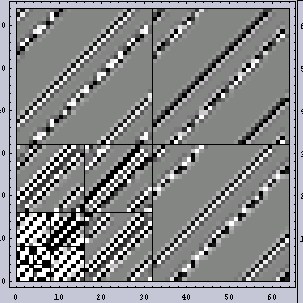
第一段階として高周波成分から調べてみる。すぐにこの結果の意味がわかるだろうか?
 |  |
| 高周波のX成分 | 高周波成分 |
| 低周波成分 | 高周波のY成分 |

もう何分割かしてみる
なお、フーリエ変換では基底関数としてSinが用いられるが、Wavelet変換では基底関数としていろいろな関数を使うことができる。今回はDaubechiesの4次のものを用いている。下がその形である。
 |
ドットのノイズを解析してみる
それでは、今回の本題に入る。以下が原画像である。左が「2つの大きなドットからなる」画像であり、右がそれにノイズの加わった「ノイズ」画像である。ここでノイズはホワイトノイズを加えているつもりである。ドットは周期性を持つデータだが、ノイズ自体は周期性を持たない所がミソである。また、ここで言う「ノイズ」とは現実の現象とは何ら関係がない。単なる例えである。 | 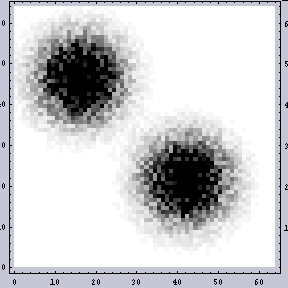 |
 | 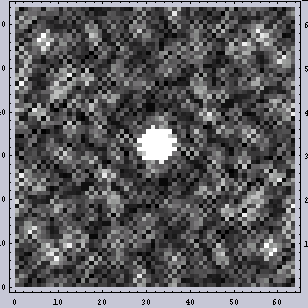 |
右のノイズの加わった画像の2DFTの結果では、広い周波数領域で強度が上がっている。しかし、下の鳥瞰図で示した(私は立体が好きなのだ)方でもわかると思うが、バックグラウンドが持ち上がっているだけである。いずれにせよ、あまり左右の間で違いはない。今回のような64x64の画像ではなく、もっと大きい画像ではその違いははより識別不能になる。
 |  |
 |  |
1999-06-26[n年前へ]
■リモートカメラから世界をノゾこう! 
Macintosh用カメラ制御プログラムを作る
今日もニュースを探しに
MAQ?MAK?MAC! ( http://www.maqmakmac.com/)
を見に行くと、おやおや何やら見たことのあるキーワードがある。これが「デジャブ」という奴かと一瞬思ったが、そうではないようだ。本WEBについての記載がある。ビックリだ。いや、ホント。
自分の興味の趣くままにやっているサイトではあるが、好きなサイトで「面白い」といってもらうと、とても嬉しい。また、そこから辿り
WebCatchを見る。「ノーラ」氏の文章には頭が下がる思いである。
MAQ?MAK?MAC!には「もっとMacintoshに関連した話題が多ければ良いのになぁ?。 」とも書いてある。そう、私もMacintoshの話題が少ないとは思っていたのだ。Macintoshが多い私の職場の人々からも(次回の話への伏線)言われ続けてきたことなのである。ならば、MAQ?MAK?MAC!( http://www.maqmakmac.com/ )登場記念にMacintoshを使った話をやってみたい。
というわけで、今回は急遽Macintoshを使った実験の話である。物語は、こんなジャンクを手に入れたところから始まる。ごくたまに、秋葉原でも見かける。もし見かけて、かつ、安かったら、迷わず「買い」だ。LEGOのMindstormsなんかと組み合わせたら、かなりかっこいいはずだ。
 |
これが、「Canon製ビジュアルコミュニケーションカメラ」である。シリアル通信でカメラの向きやズームピントを変えることができるものである。上下左右に首を振ることができるし、ズームやマクロ撮影も可能だ。発売当初は20万円位もしていたものだ。この後継機種も出ている。
これを使って、何か面白いことをしてみようと思った。いや、はっきり言ってしまえば、ネットワーク上のMacintoshにこのカメラをつなげて、それを他のコンピュータから制御しようにしたい。今でこそ、そういったWEBサイトも多々あるが、今回の話の実験を行った時(確か2,3年前)にはまだ少なかったのだ。
このカメラはジャンクとして手に入れたので、ソフトも何も付いていない。しかし、シリアル通信のコマンドは何とか判明したので、制御プログラムを作ってみた。といっても、単なるシリアルポートへコマンドを送りつけるプログラムである。
プログラムはここに置いておく。名前もずばり、「のぞき見君」である。もちろん、Macintosh版なのでWindowsでは使えない。
のぞき見君 0.1anozokimi01a.sit ( sit形式 332kB )
正式にこのカメラを持っているユーザーにも今回のような用途(イヤな用途である)であれば、このソフトはきっと役に立つと思う。
今回(といっても作成したのはずいぶん昔だ)作成したプログラム「のぞき見君」の起動画面が下である。
 |
下がメニュー画面である。画面を見れば判ると思うが、全てのメニューをコマンドキーを用いてキーボードのみでコントロールするようにしてある(これが素早く使うためのミソだ)。
 |
このソフトをインストールして、Macintoshとカメラをシリアルポートでつないで、また、ビデオ出力もMacのビデオ入力につなげばとりあえず、接続完了だ。これで、Macintoshから自由自在に制御できるビデオカメラの完成だ。
さて、次はネットワーク経由で制御するための作戦だが、何ら苦労(私の)は必要ない。例えば、innfo-macに登録されているremote-mouse-keysというようなソフトを使えば、ネットワークにながっているMacintoshのキーボードやマウスを制御することが簡単にできる。
ftp.flashnet.it/mirror/8/sumex-aim.stanford.edu/comm/remote-mouse-and-keys-10.hqx
ビデオ画面の転送はもちろん、Cu-SeeMeでも使えば良い。最近はその手のソフトも多いだろう。それでは、今回のプログラム群を使った構成図を以下に示す。Macintoshはネットワークの自由度が高いので色々な使い道がある。
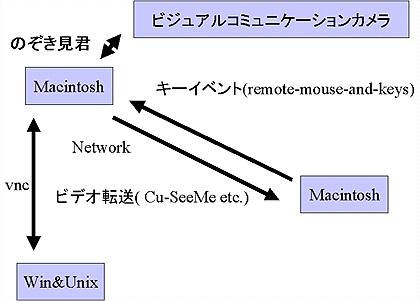 |
remote-mouse-keysとCu-SeeMeの組み合わせが軽くてお勧めなのだが、今なら
vnc (http://www.uk.research.att.com/vnc/index.html )
を使うといったやり方もアリだろう。これなら、プラットフォームをあまり選ばないので、WindowsやUnix系OSからでも制御できるし、一つのソフトで制御もビデオ画面転送も済んでしまう。ただし動作がまだ重いとは思う。
それでは、今回のソフトを使った顧客例を紹介しよう。
それは私の職場の「ち*の」氏の使用例である。彼は結婚間近であった。いずれ妻と住む新居にPowerMacintosh6100がこのカメラとともに設置してあった。彼は家の戸締りが気になって、職場から家にPPP経由でRemote-Accessを試みた。彼のPowerMacintosh6100は電話がかかってくるとともに起動音を発し、起動した。そして、彼は職場からの制御により、家のPowerMacintosh6100につながったカメラは首を起こし右へ左へと方向を変え、戸締りのチェックを始めた。彼の目的は達成された。家の戸締りは完璧であった。
ただ一つの問題は、彼は知らなかったが、結婚間近の恋人が掃除をするために新居を尋ねていたことである。彼女の目の前で、電話の音とともに勝手にMacの電源が入り、「ジャーン」という音を発し、そして、そこにあるカメラが「ウィィィーン、ウィィィーン」と右へ左へ動き始めたのである。「ひどい恐怖を感じました」、と彼女は後に語ることになる。
その後、彼の結婚がはたして実現したのか、それとも実現しなかったのかはここでは明らかにしない。
1999-08-14[n年前へ]
■年始は景気が悪いの法則 
株価・為替グラフ表示ソフトを作ろう
自慢ではないが、私は経済には疎い。しかし、霞を食べて生きているわけではないので、勤務先の景気の行方は私の食生活を左右してしまう。その年の給料は年始に労使交渉の後に決まるのだが、何故か毎年その時期は勤務先の景気は悪いのである。当然、毎年不景気な労使交渉が行われることになる。
「何故か毎年その時期は勤務先の景気は悪い」と書いたが、わかっている理由もある。例えば、その前年末に売れてない製品を売れたことにして前年の売上に押しこめてしまうから、次の年始は当然製品の売れ行きが下がるわけである。従って、給料を安く抑えるためには、労使交渉を年始に行うのがいいと思われる。
そういうことはおいておいても、経済の勉強は少しはしなければならないだろう。こう思ったきっかけは、「今日の必ずトクする一言(http://www.tomoya.com/)」の
- 株価の先読みは可能か?(風水学的に店頭市場を見る編)
- (http://www.bekkoame.ne.jp/~jh6bha/higa9904.html#990427)
それでは、今回のサンプルには「カシオ計算機(株)」を使うことにしてみる。まずは、カシオ計算機の株価の最近一年間の変動を以下に示してみる。
 |
さて、これだけでは何がなんだかわからないし、カシオ計算機の特徴もわからない。
- 他の会社の平均に対してカシオ計算機の特徴はどうか?
- カシオ計算機の株価と相関があるパラメータは何か?
他の会社の平均を調べるためには、日経平均株価を見れば良いのだろう。そして、カシオ計算機のような輸出を主体とする製造業の場合は、円vsUS$為替が株価と極めて相関が高いことが多いので、日経平均株価と円vsUS$為替の変動を示してくれるサイトがあれば簡単に比較ができるだろう。例えば、そういった情報はYAHOOやASAHI..COMから得ることができる。
しかし、大雑把に探した限りでは、日経平均株価と円vsUS$為替の変動を同時に表示してくれるサイトが見当たらなかった。そこで、日経平均株価と円vsUS$為替の一年間の変動を表示するソフトウェアEconomicを作成することにした(経済の勉強から離れてしまっている気もするが...)。
プログラムの内容はごく簡単で、ASAHI.COMにアクセスして「日経平均株価」と「円vsUS$為替の変動」を示す画像を取得して、合成するだけである。今のところ、proxy対応にはしていないが、そうするのもごく簡単なので、気が向けばproxy対応にするつもりだ。
また、動作のためにはSUSIEプラグインのJPEG対応プラグインを必要とするので「Susieの部屋」から適当なプラグインをダウンロードし、Economicプログラムと同じディレクトリか、システム、もしくはSUSIEアプリケーションのあるディレクトリに入れておく必要がある(経済の勉強をするのに、何故SUSIEプラグインの話になるのだろう? というツッコミは無しだ。)。Economicプログラムは以下からダウンロードできる。
 緑 : 円vsUS$為替 紫 : 日経平均株価: |
- 他の会社の平均に対してカシオ計算機の特徴はどうか?
- カシオ計算機の株価と相関があるパラメータは何か?
それでは、このEconomicを用いて、カシオ計算機の株価の変動を見てみよう。
 |  |
見比べてみると、カシオ計算機の株価は日経平均株価(左の紫の線で示してあるもの)とはあまり相関が無い。日経平均株価が右上がりで高くなっているのに対して、カシオ計算機の株価は最初に大きく低下した後に、低迷を続けている。
それに対して、円vsUS$為替の変動(左の緑の線で示してあるもの)と見比べてみると、ほぼ同じであることがわかる。輸出を行っているメーカーはどうしてもこうなってしまう。例えば、1円円高になると為替で数十億円も損失が出たりするのである。素晴らしい製品を作るかどうかよりも、円高になるか円安になるかの方が重要であったりするのだ。しかも、(私の気のせいだとは思うが)いつも年始は円高で、そのため毎年給料が不景気になるような気もするのだ。困ったものである(私が)。
さて、こういったプログラムは作るのが簡単な割に面白い(私としては)ので、色々と応用プログラムを作成して遊んでみるつもりである。そうして、いつか経済オンチを克服してみたいと思うのであった(経済の話なんかほとんど出てきてないような気もするが...)。