1999-12-27[n年前へ]
■恋の力学 三角関係編 
恋の三体問題
今回はもちろん、
の続きである。前回は、恋の力学を二体間の単純問題に適用したが、今回は複雑系の入門編である三体問題に適用してみたい。二体間の単純問題から三体問題になることで、現実問題に近くなる。また、物語性も大幅にアップする(当社比)。その物語性のいい例があるので、簡単に紹介しておく。小山慶太の「漱石とあたたかな科学」講談社学術文庫の第七章に面白い話がある。- 「明暗」とポアンカレの「偶然」 - である。漱石が、明暗の中でのモチーフにしている「ポアンカレの説明する偶然」について、
- ラプラス -> ポアンカレ -> 漱石
「明暗」の中での登場人物
- 津田
- お延
- 清子
前回の「二体間の単純問題」というのは、「無人島で男と女が二人きり」という舞台設定である。現実にはあり得ない。あぁ、しまった。こう書くと、まるで今回の「三体問題」は「無人島で男二人と女一人」という舞台設定に思えてしまう。これだって現実問題としてあり得ないような気がしてしまう(関係ない話ではあるが、「無人島で男二人と女一人」という舞台設定で始まるジョークは「アメリカ人なら男同士が殺し合い、イギリス人なら紹介されるまで口をきかないから何も起きず、フランス人なら片方は恋人で片方は愛人になり問題は起きず、日本人ならホンシャにどうしたらいいか訊く。」というオチだったように思う。うーん、言い返せない。)。
だが、都会という砂漠が舞台であると思えば、東京砂漠に「男二人と女一人」、あるいは「男一人と女二人」といったような舞台設定は無理がないだろう。そう舞台は東京砂漠ということにしておこう。
それでは、考察を行ってみることにする。まずは解析の条件である。「男」と「女」に関する「恋の力」は前回と同じく、
- 「恋の力」 = 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「同性に対する反発心」 = 「相手の魅力」 * 「二人の間の距離ベクトル」/ 「二人の間の距離スカラー」
- 「恋の力」-「同性に対する反発心」 = 優柔不断度 * 「恋の加速度」
それでは、以下に計算結果をグラフにして示してみる。まずは、「女」「男1」「男2」全員が同じ資質を持つ場合である。この場合、「三すくみ」状態に陥る。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
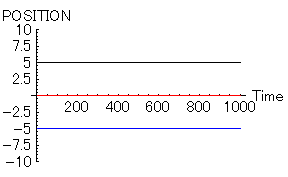 |
この「女」を中心にして、「男」達が身動きが出来なくなった状態はよく見かけると思う。ねるとんなどでよく見かける風景である。ただし、この状態が発生している理由は「男1」と「男2」そして「女」の魅力が全く同じ状態であるからだ。
ほんの少しでも「男1」と「男2」に有利な点があれば、この状態は一変する。次に示すのは「男1」が「男2」よりも1%だけ魅力がある場合である。その1%は理由は何であっても良い。例えば、偶然駅で出会ったなどでも良いだろう。
- 「女=赤」 位置=0, 速度=0,魅力=10,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10.1,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
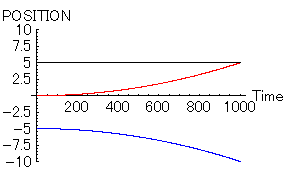 |
その一方、「男1」と「女」は幸せイッパイだろう。クヤシイくらいである。全く...
また、「女」に大きな魅力があった場合には、先の「三すくみ」状態ではなく、見事な「三角関係」に陥る。これは、三すくみ状態を打破するのに十分な魅力が「女」にあるからである。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10,優柔不断度=10
 |
「女」を中心にして「男1」と「男2」が右往左往する様子が手に取るように分かる。これも世の中にはよくあるケースだろう。涙無しには見ることのできないグラフである。いや、もしかしたら、私の周りだけかもしれないが...
もちろん、この場合も「男1」と「男2」の魅力にほんの少しでも違いがあれば、状態は一変する。今度は「男2」に「男1」よりも1%魅力が多くあるものとしてみよう。
- 「女=赤」 位置=0, 速度=0,魅力=20,優柔不断度=10
- 「男1=黒」 位置=5, 速度=0,魅力=10,優柔不断度=10
- 「男2=青」 位置=-5, 速度=0,魅力=10.1,優柔不断度=10
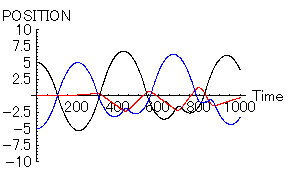 |
「女」の心が「男1」と「男2」の間で揺れ動いている様子がわかると思う。「男」は「恋の力」と「同性に対する反発心の力」により、右往左往状態である。これぞ、リアルな三角関係である。この場合、果たして「男1」が勝つのか「男2」が勝つのか、よくわからない。どの時点で「勝ち」を決めるかで大違いである。また、「女」にすらその結末は予想できないのではないだろうか。「女」自身も相手を決めた本当の理由はわからないと思われる。
これは、もう複雑の極致であるが故に、何の予想もできないのである。
ここまでの話はまるで天文学者が頭を悩ます三体問題のようである(いや、もちろんあちらが本家だが)。天文学者は天体の三体問題に頭を悩まし、我々は恋の三体問題に頭を悩ますのだ。どちらも、実にロマンチックである。
こうして、今回の話の結末はよくわからないままになってしまった。やはり、ここは「明暗」の津田のつぶやき、
「偶然? ポアンカレのいわゆる複雑の極致?なんだかわからない」という言葉で締めくくろうと思う。漱石は偉大である。
さて、「恋の力学」シリーズはまだまだ続く。近日公開とはならないかもしれないが、次回作の予告をしておこう。
- 恋の力学 運命の人編 - 偶然と必然の境界線 - (仮称)
2000-01-03[n年前へ]
■音場の定位を見てみたい 
立体音感を考える その2
前回(といっても間に他の話も挟まっているのだが)、
で「音の立体感」について考え始めた。今回はその続きである。「音の立体感」を考えるための道具を作る準備をしてみたい。色々なことを考えるには、その目的にあった測定器が必要である。何か新しいことをしようと思ったら、そのための新しい測定器を作成しなければならない(と思うだけだが)。そして、何より私は計測器なんてほとんど持っていない。だからといって、計測器を買うお金があるわけではない。というわけで、困ってしまうのだ。
そこで、立体音感を考えるための測定器を作っていくことにした。といっても、すぐにできるとも思えないので、色々実験をしながらボチボチとやってみることにした。勉強がてら、ボチボチやってみるのである。オーディオ関連のことにはかなり疎いので勉強にはちょうど良いだろう。
資料をいくつか眺めてみたが、特に
- 「立体視の不思議を探る」 井上 弘著 オプトロニクス社
- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
そこで、いきなりだが今回作成した解析ソフト「音場くん一号」のアルゴリズムは以下のようになる。
- PCのサウンド入力から、サンプリング周波数 22.05kHz、Stereo 各チャンネル8bitで取り込みを行う。
- 取り込んだデータを4096点毎にウィンドウ(Hamming or無し)処理をかける。
- 高速フーリエ変換(FFT)を行う
- FFTの結果の実部について、左右のチャンネルの差分を計算する
次に示すのが、「音場くん(仮名)一号」の動作画面である。「音場くん(仮名)一号」の画面構成は、
- 右側->制御部
- 左側->計測データ表示部
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
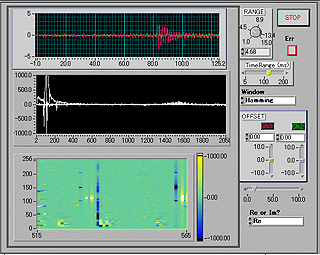 (黒字に赤、緑の色構成は変更の予定) |
計測データ表示部の拡大図を下に示す。
- 音声波形データ(赤=左、緑=右)
- 周波数(横軸)vs左右での音圧の差(縦軸)
- 時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)
この表示計の意味を例を挙げて説明したい。例えば、下の画面では左の方に定位している音が鳴ったときの状態を示している。一番上の音声波形データでは緑(右)の波形は小さいのに対して、赤(左)の大きな波形が見えている。
また、真ん中の「周波数(横軸)vs左右での音圧の差(縦軸)」では横軸100(任意単位)程度の高さの辺りで左チャンネルに位置する音が発生しているのがわかる。
また、一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」では時間的に一番最後(横軸で右側)の方の横軸560、縦軸100位の位置に白い(すなわち左チャンネルに定位する)音が発生しているのがわかると思う。
 |
この曲のイントロでは、「ポンッ」という音が高さを変えつつ、左右にパンニング(定位位置を変化させること)する。
一番下の「時間(横軸)vs周波数(縦軸)vs左右での音圧の差(色)」を示したグラフ中で白・黄色(左に定位)と青・黒(右に定位)する音が時間的にずれながら現れているのが判ると思う。
このようにして、この「音場くん(仮名)一号」では音の定位状態についての「極めて大雑把な」計測が可能である(保証はしないけど)。「音場くん(仮名)一号」を使った他の例を示してみる。
下は種ともこの「O・HA・YO」の中から「The Morning Dew」のイントロ部を示したものだ。
- 左(白・黄)チャンネル方向に定位するピアノ
- 右(黒・青)チャンネル方向に定位するガットギター
 |
これはまるでオルゴールのピンを見ているようだ。あるいは、シーケンサーや昔の自動演奏ピアノのロール譜のようである。対位法などの効果をこれで確認したくなってしまう。
さて、ここまでの例は楽器も少なく、比較的自然な定位状態であった。しかし、以下に示すような場合には不自然なくらいの「音の壁」状態の場合である。かなり状態が異なる場合だ。
 |
これは、種ともこの「O・HA・YO」の中から「KI・REI」のラストのラストコーラス部を示したものである。人のコーラスが重なり合っていく部分である。色々な高さの声が重なり合っていく様子がわかるだろう。
ところが、このグラフをよくみると、同じ音が時間的に持続しているにも関わらず、時間毎に定位位置が左右で入れ替わっているのがわかる。
これはきっとエフェクターで言うところのコーラスなどをかけたせいだろう(素人判断だけど)。人工的にフィルタ処理をしているためにこのようになるのだろう。こういう結果を見ると、「音場くん(仮名)一号」をプログレ系の音の壁を解析してみたくなる。
さて今回は、音声の定位状態を解析する「音場くん(仮名)一号」を作成し、いくつかの音楽に対して使ってみた。まだまだ「音場くん(仮名)一号」は作成途中である。これから続く立体音感シリーズとともに「音場くん(仮名)」も成長していく予定である。
さて、一番先の画面中に"Re"という選択肢があるのがわかると思う。もちろん、これと対になるのは"Im"である。FFTをかけた結果の"実部"と"虚部"である。"実部"の方が左右の耳の間での音の大きさの違いを示すのに対して、"虚部"の方は左右の耳の間での位相差を示すものだ。つまり、ある周波数の音が左右の耳の間でどのような位相差を示すものか、測定しようとするものである。
左右の耳に対する音の位相差というものは、立体音感を考える上では避けては通れないのだろう。しかし、位相差を処理しようとすると、どうしたらいいものかかなり迷う部分がある。また、今回のようなFFT処理をかけたときに得られる位相を用いて良いものかどうかもよくわからない。というわけで、今回は位相解析処理は後回し、ということにした。
2000-01-08[n年前へ]
■着メロの音響工学 
この着信音は誰のだ!? 立体音感その3
街中で携帯電話の着信音が鳴ると、周辺の人が一斉に自分のポケットを探る光景というのはよく見掛ける。それは、まるで「クイズ・ドレミファドン」のようである。そう「超・イントロクイズ」そのものなのだ。「このイントロはオレのか!?それとも!?」と皆が考えている瞬間である。
着メロのイントロが始まるや否や、腰の携帯電話に手をやる様子は「おまえは荒野のガンマンか!」とツッコみたくなる程である。
特に、私の勤務先などでは全員が同じPHSを持ち歩いているせいか、着信音が聞こえ始めると、みな自分のポケットを探り始める。もちろん、そのPHSの着信音は数種類ある。しかし、1500人程度の従業員がいるわけだから、1500人/ 数種類だけ同じ着信音があるわけだ。仮に15種類あるとしても、
1500(人) / 15(種類数) = 100(人/種類)つまり、自分と全く同じ着信音のPHSを持つ人が100人もいるのだ。世の中には「自分と同じ顔の人が七人いる」というが、職場に同じ着信音の人が100人もいるのである。これでは、着信音が鳴ると同時に多くの人がポケットを探るのも自然だろう。
もちろん、この解決策として、「着信音でなくてバイブレーターを使う」というものがあるわけだが、何故かその解決策は許されないらしい。不思議である。
さて、そもそも、何故自分の着信音を区別できないのだろうか? まず、その辺りから考えてみることにする。
着信音が鳴ったときに、「自分の着信音かどうか判断するための基準」は二つあるだろう。それは、
- 着信音の種類
- 着信音が鳴っている位置
着信音の鳴っている位置 = 自分の携帯電話の位置が成立するかどうか即座に判断できれば、着信音が同じでも「自分の着信音であるか」の判断が可能ということだ。
つまりは、「携帯電話の着信音という音源の定位」という問題を考えれば良いことになる。もし、「着信音の定位」が判れば、自分の携帯電話の着信音か他の人の着信音かどうかなんてことは考えなくて済むのだ。そう、今回は「立体音感」シリーズその3だったのである。
それでは、一体「着信音がどこで鳴っているのか、すなわち、着信音の定位」が判るためには何が必要なのだろうか?
前回、
で「音の立体感に関する因子」について- 音像定位の因子
- 両耳差因子 (音響信号)
- 音の強さ(振幅)の差
- 位相の差
- 周波数スペクトル因子
周波数スペクトル因子というのは、例えば、
の中の記述指を前方で鳴らしてみて下さい。 そしてすこしずつ手を頭の側方に、手と頭の距離を変えないようにして、移動してみて下さい。 音量がわずかに大きくなったこととある特定の中域および広域の音がより強調されることに気が付かれるでしょう。 この実験では、指を鳴らす動作は一定の音量と周波数を発生する音源として用いられたわけです。 耳は同一の音源が前方から来る場合と、側方から来る場合で全く違う音と聞き分け、頭脳にそれを登録します。 側方の音は若干大きく、また耳たぶのせいで高い周波数で聞こえます。にあるようなものである。
音波が人間の頭部を通過してくる間に音波の周波数分布が変化し、その変化具合で音波がやってきた方向を知ることができるというものだ(多分)。もちろん、位相分布も変化するだろうが、ここでは周波数分布しか考えない。
こういう音像定位の因子における「周波数スペクトル因子」を考える時に、もし音源の周波数スペクトルがごく狭いものだったらどうだろうか?つまり、単一の周波数しか含まない音源だったらどうだろうか?周波数スペクトルが変化するといっても、単一のスペクトルしか含んでいないのだから、振幅が変化する効果しかない。周波数スペクトルの分布は何ら変化しない。
ということは、「音像定位の因子における周波数スペクトル因子」が上手く作用しないことになってしまう。(もちろん、実際には非線形な効果が存在するだろうから、多少は周波数スペクトルも変化するとは思うが。)
これと全く同じことはまたしても「物理の散歩道」で触れられている。ロゲルギスト著の岩波新書「第四物理の散歩道」の「不規則なものの効用 三節」である。純音より不規則な音の方が「立体感」を得られるだろう、と書いている。
今回、「携帯電話の着信音の定位」を「着信音のスペクトル分布」という観点から調べてみることにする。携帯電話の着信音がどのような波形であるか、どのような周波数分布を持っているかを調べるのである。果たして、携帯電話の着信音の周波数分布はどうなっているのだろうか?(部品点数を考えれば、ほぼSin波か矩形波なのが当然だろうが...)
まずは手持ちの機種で着信音の波形とスペクトルを見てみることにした。使った機種を以下に示す。
 |
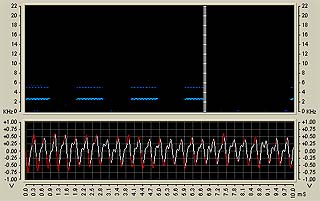
それでは、着信音No4と着メロ「この木何の木」の波形とスペクトログラムを次に示す。それぞれのグラフ中で上は「時間vs周波数分布」を示すスペクトログラムであり、下は「時間vs強度」の波形グラフである。
まずこれが、着信音No.4の波形とスペクトログラムであり、
 |
こちらが、「この木何の木」の波形とスペクトログラムだ。
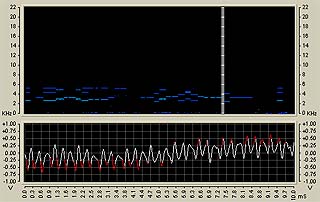 |
どちらも周波数分布はそれほどブロードではない。すると、「音像定位の因子における周波数スペクトル因子」を用いた「立体音感」がうまく働かないかもしれない。ただし、着信音No.4に関しては時間的に変化しないが、着メロ「この木何の木」に関しては、当然だが時間的に変化していく。
この違いが果たして、「着信音の音像の定位」の判断を左右するものか、自分の耳で実験することにした。着信音No.4と着メロ「この木何の木」を鳴らした時に、どこから鳴っているように聞こえるか判断してみるのだ。
目をつぶり頭の周囲で着信音を鳴らし、その定位を判断してみた。すると、色々な着信音を聞いてみたがいずれも定位の判断がしづらかった。特に頭の前後の判断がしづらい。それは、着信音No.4と着メロ「この木何の木」でも同様であった。やはり、純音に近いと「音像定位の因子における周波数スペクトル因子」が働きづらいのかもしれない。
そして、着信音No.4と着メロ「この木何の木」だが、むしろ着信音No.4の方が判断をしやすかった。メロディだと音が変わるときに定位が変わるかのような感覚を受けた。そのため、判断をしにくかった。もちろん、これは私だけの感覚かもしれない。その辺りは被験者を増やして実験をしてみたい(再実験をする日が来るかどうかは大いに疑問であるが)。
また、もしかしたら着信音No.4の方が矩形波に近く、純音でないのが良かったのかもしれない。もしかしたら、の話だけれど。
もし、今回使った音を聞いてみたい人がいるならば、
これを聞いてみてもらいたい。ただし、サイズがでかいので要注意だ。あとバックグラウンドがうるさいのはハードディスクとファンの回転音である。困ったものだ。 最近多い「同時発声数が多い着メロ機能」というのも、使って実験すると面白そうだ。しかも、音が分厚いヤツがあると、案外良いモノかもしれないな、とうらやましく思ったりするのである。そして、着信音スピーカーがプアァで歪んでいる機種なんかが、色々な周波数成分を含んでいて、実は「着信音の定位」に関しては良かったりするのかもしれない、と考えたりする。しかし、こちらはチットモうらやましくないのであった。
2000-02-19[n年前へ]
■携帯電話の同時性? 
競馬の写真判定とパノラマ写真 その後
先日
を書いてから面白いメールを頂いた。その一部を抜粋すると、小生は超音波を利用した新しい流体場測定を行っていますが、この方法で得られるDataは空間1次元時間1次元の2次元データです。従って得られるのは、このページにあったような画像が直接得られるわけです。とある。この方法といくつかの結果を発表してから、あちこちからコンタクトがありましたが、その中の一つが、NYのSirovichという高名な流体力学者からの手紙でした。彼はいわゆるSnapShotを、逆に小生のデータから構築できないか、というのです。
今このWebでされたことの逆をしたいというわけです。流れの空間構造を解析するために使いたいのです。残念ながらこれは、以下に少々説明するように、原理的に無理な話で断らざるをえませんでした。
つまり、時間軸に速度をかけて空間軸に変換できればよいのですが、流体場はそれ自身が速度分布を持っていますから、一体何を使えば良いのかが定まらない。
電磁波の場合には光速が一定ですから、時間情報から空間情報を得ることができますが、古典流体力学では不可能なのです。工学的には平均流速を使って、時間-空間の変換をしますが、それはインチキとまでは言わないまでも、便宜的なも
のでしかありません。このWEBの中での例では、馬?の速度のみであとは静止しているので、可能でし
ょう。
「馬?」という箇所に、私との意見の相違があるようだ。私が明らかに「馬」であると言い張っているものに疑問を持たれているような気がするのであるが、今回そこは気にしないでおく。
なるほど、音波や電磁波などを使って計測を行い、得られた
- 空間(あるいは量)-時間
- 空間(あるいは量)-空間
- 海の中の魚を探知する「魚群探知機」
- 気象状況を計測する「気象レーダー」
- 固体の中の電荷分布を計測する「電荷分布測定装置」
「魚群探知機」は超音波を水中に発信して、その反射波が刻々と帰ってくる様子から、(超音波の速度を用いて、空間位置に変換した後に)障害物(ここでは魚群)の様子を計測するものである。「気象レーダー」も電波を使って同様に雲の分布などを測定する。
「電荷分布測定装置」の場合は、(例えば外部電界を印加し)電荷を持つ個所を振動させてやり、その振動がセンサー部に刻々と伝わってくる様子から(あぁ、なんて大雑把な説明なんだ)、(固体中の弾性波の速度を用いて、空間位置に変換した後に)固体の中にどのように電荷分布が存在しているかを計測するものである。
と、文章だけでは何なので、WEB上から、それらの計測器を用いた場合の計測例を示してみる。
下が魚群探知機である。リンク先は
である。 |
また、この下は空間電荷測定装置である。これなども、とても面白いものだ。リンク先は
である。 |
さて、こういうことを、調べてみるだけではしょうがない。自分でもそういう計測をしてみたい。
そこで、次のような実験をしてみようとした。
- 部屋の中に複数の「音の発信源」を配置する。
- 複数の「音の発信源」から同時に音を発する。
- それをPCで収録する。
- 音声が「音の発信源」からPCに到達するまでの時間を解析する
- 複数の「音の発信源」の位置を計測する。
そこで、安易にも時報を使おうかと考えてしまった。しかも、数があって手軽ということで、携帯電話を使おうとしたのである。
しかし、複数の携帯電話を集めて、117に電話して時報を同時に聞いてみると、とても同時どころではない。てんでばらばらなのである。電話のスピーカーから流れてくる時報のタイミングには結構ズレがあるのである。
携帯電話の間には結構同時性がないのだ。また、固定電話とも比較したが、固定電話よりも時報が速いものもあれば、遅いものもあった。
そこで、複数の携帯電話を聞き比べた結果を以下に示してみたい。この写真中で左の携帯電話ほど時報が先に流れており、右になるほど時報が遅れているのである。一番早い左と、一番遅い右では一秒弱の違いがあった。
 |
また、参考までに、家の固定電話と携帯電話の時報を一緒に聞いたサウンドファイルを示しておく。
この携帯電話は先に示した画像の一番左である。つまり、先の携帯電話群では一番時報が早かったものなのである。しかし、家の電話よりは一秒弱遅かった。ということは、家の固定電話と先の一番遅い携帯電話では時報の時間にして2秒弱の違いがあることになる。 そして、「家の固定電話と携帯電話の時報を一緒に聞いた音の変化」をスペクトログラムにしたものを以下に示す。
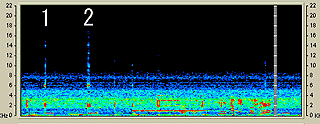 |
水平軸が時間軸であり、時間は左から右へ流れている。また、縦軸は音の周波数を示している。ここでは、「1」で示したのが家の固定電話の時報であり、少し遅れて「2」の携帯電話の時報が聞こえているのが見てとれる。
よく時報を確認することはあるが(実は私はほとんどないのだが...)、携帯電話・PHSで時報を聞く限り、秒の精度はそれほどないようである。また、勤務先の固定電話は先の携帯電話群と比べても遅い方であった。それは少し意外な結果であった。
今回調べた「携帯電話の同時性のなさは」は常識なのかもしれないが、電話の時報で時計を合わせるのはあまり精度が出ないやり方であることがわかっただけでもよしとしよう(別に実験を途中で投げ出した言い訳ではないけれど)。
今度、TV(衛星TVなども遅延時間を考慮した時報の放送を行っていると聞くし)やラジオを用いて当初計画していた実験を行おうと思う。その際には、時報がPCに到達する時間のズレで「音の発信源」までの距離を計測し、左右のマイクでの違いを計測することにより、「立体音感シリーズ」のように「音の方向」を得てみたい。
というわけで、話が「立体音感シリーズ」に繋がったところで、今回は終わりにしようと思う。
2000-05-13[n年前へ]
■ミウラ折りの落書き紙 
思ったことを折り込めて
十年位前のことだったと思う、「知人の先生がこんなのを作ったんだけど、興味あるだろう?」と父が不思議な冊子を私にくれた。冊子と言っても、それは一枚の紙を折り畳んだ小さな小さなものだった。ちょっと面白い折り畳み方をされたその紙には、その折り畳み方の説明とその「折り畳み方」の応用が書かれていた。もちろん、その冊子の作者は宇宙科学研究所の三浦教授で、そしてその冊子の折り畳み方はあの有名な「三浦折り」である。
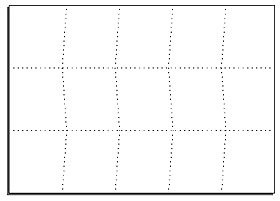
三浦折りの折り目を示してみると、例えば下の図のようになる。一目見てわかるように折り目が直交していない。そのため、それぞれの折り目が独立でなく、全ての折り目が同期しているのである。言い換えれば、一つの折り目を開こうとすると全ての折り目が開いていくし、一つの折り目を閉じようとすると全ての折り目が閉じていく。だから、例えば、折り目の端っこと端っこを掴んでただ引っ張れば全ての折り目が開き、そして折り目の両端を縮めれば自動的にパタパタと折り畳まれていくのである。
また、折ってみるとわかるのだが、この三浦折りは折り目が少しづつずれて重なるのである。折り目というのは厚みが他の部分に比べて厚いために、折り目が重なるとその部分だけがどうしてもかさばってしまう。しかし、この三浦折りであればそんな折り目が重ならないので、折り畳んだときにかさばらないのである。
 |
だから、太陽電池パネルなどをこんな三浦折りを使って折り畳むと、折り畳んだときにはかさばらないし、その展開や収納は隅と隅をただ引っ張ったり縮めたりしさえすれば良い、というわけで良いことずくめというわけだ。詳しくは、宇宙科学研究所のここ辺りを読んでもらうことして、参考までにそこの画像にリンクを張っておく。
 |
ところで、十年前に父からもらった「三浦折りの冊子」を捨てるはずはないから、部屋のどこかに隠れているとは思うのだけれど、何処かに隠れてしまっていて、見つけることができなかった。私の部屋が三浦折りのようになっていて、部屋の隅から隅までを全て引っ張り出すことができたら、きっとすぐにでも見つけられたのだろう。しかし、残念ながら私の部屋は三浦折りではないのである。だから、私の色々なモノや本が散らばった部屋に隠れている「三浦折りの冊子」はそう簡単に見つけられるわけもない。
そういえば、ふと何かが心に思い浮かぶことも日頃よくあることである。しかし、思い浮かんだその時に書き留めておかないと、すぐに記憶の何処かに隠れてしまって忘れてしまうことも多い。これもまた、私の記憶が三浦折りだったらよいのだろうけれど、幸か不幸か私の記憶システムは三浦折りではない。私の記憶や考えたことが三浦折りのようにパタパタ開かれていくのも見てみたい気もするけれど、隠しておきたいような夢や気持ちもあるだろうから、やはり私の記憶システムが三浦折りでない方が良いのだろう。
とはいえ、やはり後で思い出したいこともたくさんあるわけで、そんなことは思い浮かんだらすぐに何かに書き留めておかなければならないだろう。落書き帳か何かに、思い浮かんだことをすぐに書き留めておけば良いわけである。適当な落書き帳に書き留めれば、思い浮かんだことを忘れてしまっても安心である。
しかし、頭に何かが浮かぶ瞬間というのは、時間や場所を選ばないだろうから、そんな落書き帳はいつも持ち歩かなければならないだろう。となると、いつも持ち運ぶためにはコンパクトでなくてはならないし、そんな落書き帳を広げる作業は簡単に素早くできなければ不便である。だとしたら、その落書き帳はまさに三浦折りを使うべきではないだろうか? というわけで、私は自分用の「落書き紙」をミウラ折りを使って作ってみることにした。
というわけで、作ってみたのがこの「できるかな?」特製「落書き紙」である。折り畳んだ状態は三浦折り特有のちょっと不思議な重なり方になり、見た感じのデザインも割に良い感じだと思う。そして、これが「できるかな?」特製「落書き紙」折り畳みのようすである。
両端を動かすだけで、パタパタと自然に開いたり折り畳まれていくようすがよく判ると思う。 | 実際の大きさは掌にすっぽり隠れるサイズ。 裏表紙は表紙を裏返したデザイン。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、という気持ちの現れなのである。 |
ここにPDFファイル化した「できるかな?」特製「落書き紙」を置いておくので、興味のある人はぜひプリントアウトして三浦折りを実際に試してみると面白いと思う。このPDFファイルは開くときにパスワードを聞いてくるが、"hirax.net"といれてやれば開くことができる。
ちなみに、この「できるかな?」特製「落書き紙」の表と裏を見てみるとこんな感じになる。裏表紙は表紙をそのまま裏返したデザインにしてある。それは、考えたり思ったりしたことにはきっと表も裏もあるだろう、そしてそれは表裏一体で単に裏表の関係なのかもしれない、という気持ちの現れなのである。 |
 |
この「できるかな?」特製「落書き紙」の作り方であるが、まずこのPDFファイルを長手綴じで両面印刷をする。そして、上下左右マージンが不揃いであれば、端部を少し切り取る。実際に折り畳んだ後であれば、そのどの程度不揃いなのかがわかりやすいから、端部を切り取る(切り取らなくても良いが)のは一番最後でも良いだろう。
そして、表の面の折り線に沿って、次の写真のように折り畳んでいくのである。
|  |
 |  |
さて、この三浦折りの「できるかな?」特製「落書き紙」は折り畳めばとても薄く小さいから、ポケットに入れていつも持ち歩いて、心に浮かんだことなどを書きとめて持ち歩くのに最適だと思う。そして、この落書き紙の裏や表に、思ったことの表から裏までを書き留める。そして、そんな思い・考えの切り抜き・断片、を小さく折り畳んだまま伝えたい人に手渡してみて、折り畳まれたもの達がその人の掌の中でパタパタと現れてくるのも、それはそれで不思議に新鮮な感覚だろう。例えば、ちょっと不思議な「三浦折りのラブレター」なんて、不思議でいい感じだと思うんだけれど… 駄目かなぁ?
