2000-02-27[n年前へ]
■「文学論」と光学系 
漱石の面白さ
前回、
でさて、モナリザと言うと、夏目漱石と「モナリサ」にも言及しなければならないだろう。と書いた。何しろ
- 恋の力学 三角関係編 - 恋の三体問題 - (1999.12.27)
- 草迷宮・空間'99 - ネコの目から見た世界- (1999.11.05)
- 「こころ」の中の「どうして?」-漱石の中の謎とその終焉 - (1999.09.10)
- 夏目漱石は温泉がお好き? -文章構造を可視化するソフトをつくる - (1999.07.14)
- [Scraps]人静月同照 - ぼくらが旅に出る理由- (1999.06.17)
その漱石は「永日小品(リンク先は青空文庫)」(リンク先は青空文庫)の「モナリサ」中で
「モナリサの唇には女性(にょしょう)の謎(なぞ)がある。原始以降この謎を描き得たものはダ・ヴィンチだけである。この謎を解き得たものは一人もない。」と書いている。女性には興味がなかったとも言われ、ずっと付き添っていた男性との関係も噂されるダ・ヴィンチである。ここらへんは、果たしてどうか?とも思う。むしろ、新宿のホストクラブのホストの方が女性(にょしょう)の謎(なぞ)については詳しいのではないかとも私は考えたりもする。
が、そんなことはどうでも良い。漱石はレオナルド・ダ・ビンチのモナリザに興味を持ち、小品を書き上げたのである。そこで、漱石とダ・ヴィンチの相似点を考えてみたい。
レオナルド・ダ・ビンチの著作には「文学論」というものがある。漱石にも同じ名前の「文学論」がある。この「文学論」はこれまで読んだことがなかったのだが、
- 「漱石の美術愛」推理ノート 新関公子 平凡社 ISBN4-582-82927-9
- 遠近法
- 漱石の文学論の「公式」
これが、とても面白い。仮名遣いが古いため、なかなか目に入ってこないのであるが、とても面白い。これは絶対に文庫本にすべきである。眺めているだけでも面白い。
まずは、冒頭のフレーズがいきなりこうである。
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。まるで、理系の教科書である。そして、目次(編)を大雑把にさらってみる。
- 文学的内容の分類
- 文学的内容の数量的変化
- 文学的内容の特質
- 文学的内容の相互関係
- 集合的F
また、「文学論」中では、例えば、浪漫派と写実派の違いについて数値的な比較を通じて述べられていたりする。実に「科学的」な思考による「文学論」である。いや本当に漱石は凄い。
さて、中の文章を解説する力は私にはない。そこで、中の図表を示してみることにする。そこで適当に思うことなどを書いてみようと思う。
次に示すのは、「文学論」の冒頭の方で「意識の焦点・波形」を説明した図である。
 漱石全集第十一巻より |
この図は人間が何かを感じるときには焦点にピークがある、そして、その周りはぼやけたものが連続的に続いているということを示したものだ。これなど、
の時の「恋のインパルス応答」を彷彿とさせる。あの時の「恋のインパルス応答」を次に示してみる。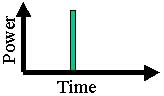 |  |
この意識される恋心(f)は先の「意識の波形」と全く同じである。ある出来事(F)と、それに付着する情緒(f)を示したものとなるわけだ。付着する情緒(f)というのは中心が一番大きく、その周りにぼやけたものが繋がっているというわけである。人間の感じ方・情緒を光学系と結びつけているわけだ。
いやはや、「恋のインパルス応答」と同じようなことを考える人はやはりいるものである。まさかそれが漱石だとは思いもしなかった。しかも時代を考えると凄まじい、としか言いようがない。
そして、さらに次に示すのは
およそ文学的内容の形式は(F+f)なることを要す。Fは焦点的印象又は観念を意味し、fはこれに付着する情緒を意味す。ということを示す図である。先の - 「漱石の美術愛」推理ノート - ではこの図と遠近法の関連が述べられている。
 漱石全集第十一巻より |
ここで、縦軸は「時間」となっており、横軸は「色々な出来事」である。ある人が感じた「色々な出来事」を時間方向に収斂させていくと、そこには「作者自身の視点がある」というわけだ。これが漱石の言う「文学論」の中心である。
この図などカメラや望遠鏡の光学系を彷彿とさせる。「光学系の一例」を以下に示す。
 |
先の「文学の焦点」を示した図はレンズで光を焦点に集めるのと全く同じだ。いや、「焦点から光を投光する」のと同じと言った方が良いだろうか。以前、
で、景色に焦点を合わせて、フィルムに結像させるのがカメラだ。しかし、フィルムに写っているのは単なる景色ではない。カメラの光が集まる焦点にフィルムが位置していると思い込むとわからなくなる。逆から考えてみれば簡単に判るはずだ。カメラの視点にフィルムが位置しているのだ。フィルムに景色が写っているのではなく、フィルムが景色を選び、景色を切り取っているのである。と書いたのと全く同じである。その光学系には歪みもあるかもしれないし、色フィルターもかかっているかもしれない。しかし、とにかく焦点にはその人自身がいるのである。写真に写っているのは、撮影者の視点なのである。写真を見れば、撮影者が、どこに立ち、何を見てるかが浮かび上がってくるはずである。フィルムに写っているのは撮影者自身なのだ。
写真でも文章でもとにかく何であっても、色々感じたことを表現していく時、その焦点には表現者自身がいる。私の大好きなこの2000/2/25の日記なんか、実にそれを感じるのである。
2000-04-01[n年前へ]
■恋の力学 恋の相関分析編 
「明暗」の登場人物達の行方
「恋の力学」シリーズである。前書き編が登場したきりで、なかなか本編に入らない「恋の固体物理学」シリーズではない。今回は、
の続き、ということになる。以前、
の中で書いたように、恋の力学シリーズは夏目漱石の影響を多大に受けている。そして、同様に夏目漱石の影響を受けているシリーズがある。それは「文章構造可視化シリーズ」である。何しろ、「文章構造可視化シリーズ」は夏目漱石をきっかけとして、始まっているのである。また、シリーズの中の話を見ればわかるように、
- 夏目漱石は温泉がお好き?- 文章構造を可視化するソフトをつくる - (1999.07.14)
- 失楽園殺人事件の犯人を探せ- 文章構造可視化ソフトのバグを取れ - (1999.07.22)
- 「こころ」の中の「どうして?」 -漱石の中の謎とその終焉 - (1999.09.10)
- 「星の王子さま」の秘密- 水が意味するもの - (1999.11.15)
そのための準備として、まずは「文章構造可視化シリーズ」で作成した"wordfreq"をバージョンアップしてみた。その動作画面を以下に示す。
 |
赤丸で示したボタンに「ファイル出力」と書いてあるのがわかると思う。つまり、文章中に「任意の単語」が出現した出現頻度を解析した結果をファイル出力する機能を持たせたのだ。1段落中に「任意の単語」が出現した数をテキスト形式で出力するようにしてある。このファイル出力結果を他のソフトに読み込めば、色々な解析ができるわけだ。いつものように、このソフトはここ
においておく。言うまでもないが、アルファ版の中のアルファ版だ。さて、今回用いるテキストは
でも登場した「明暗」である。そこで、「青空文庫」から「明暗」の電子テキストをダウンロードした。そして、バージョンアップした"wordfreq"で- 津田
- お延
- 清子
- 吉川
 |
しかし、これだけでは、よくわからない。せいぜい「清子」が小説の後半(といっても、未完であるが)に登場しているなぁ、という位だろう。しかし、さらに解析を加えてみると、もう少し面白いことがわかる。
今回は、これらの登場人物間のお互いの関わりを調べたいのである。であるならば、これらの「登場人物」の出現分布の間の相関を調べてみると面白いだろう。互いの関係を示す「相関」を調べてみるのである。異なる「登場人物」が同じような出現をしているならば、それは無関係ではない。きっと、その登場人物の間には何らかの関係があるに違いないのだ。
そこで、「明暗」を時系列的に6つの部分に分けて、津田と他の登場人物の出現分布間の相関を調べてみたのが次のグラフである。
 |
このグラフでは、横軸が時系列であり、縦軸が相関を示している。縦軸で上になればなるほど相関が高い、すなわち、「関係がある」のだ。「相関」は本人の場合で「1」である。だから、例えば最後の部分の清子の「0.6」という結果は関係がアリアリということを示しているわけだ。
また、「清子」と「吉川(ここでは夫人を意図している)」の相関が逆であることが面白いだろう。「吉川」が活躍(暗躍?)した後に、「清子」が登場するわけだ。
そして、この「明暗」が盛り上がっていくようすすら、見えてはこないだろうか?全く血の通っていないPCが解析した結果が、漱石の描こうとした「こころ」の動きを読みとっているような気が(少しは)しはしないだろうか?そして、このグラフの延長線上に、漱石の描くはずだった、「明暗」の結末はあるはずなのだ。
さて、このグラフを見ていると、
で計算した恋の多体(三体)問題の計算結果を思い出してしまう。 |
漱石は、きっと恋の三体問題を意識しながら「明暗」を書いたのである。だから、ある意味当然なのではあるが、科学と文学の一体化した世界が感じられ、とても面白い気分である。さて、この解析結果を元にして、まだまだ色々とやってみたのであるが、それは次回である。
2000-09-02[n年前へ]
■もうすぐ二歳の「できるかな?」 
初心に帰ってみましょうか?
「できるかな?」が始まったのは二年近く前の秋のことだった。
でも触れたが、当初(実は今も続いているが)は某社内の某サーバー内でこっそりと始めてみたのだった。それから二年あまりでずいぶんと色々な話が増えた。某社サーバー内でしかアップしていない- プリンタドライバーは仮免
- 続 電子写真プロセスを分数階微分で解いてみよう
- 続々 電子写真プロセスを分数階微分で解いてみよう
そして話が増えてきたせいか、自分自身でも「アレッ、あの話はどこにあったけ?」というように迷ってしまうことが多々ある。迷うどころか、最後まで見つからないこともしばしばあるのだ。そして、それは私でもない他の人であればましてやそうだろう。というわけで、
では簡単にそれまでの話の紹介をしたし、ではhirax.net内の全文検索機能を付けてみた。今回は、これまでの話題をもう一度自分で読み直して、その中から「自分のお気に入り」を調べてみたいと思う。そして、最近少し話題が変になってしまっている反省をして、もう一度初心に帰ってみようと思うのだ。
まずは、1998年の話題からいくと
というあたりが、良い感じだ。京都の風物詩である「鴨川カップル」達が人目を気にしながら寄り添う合う姿を考えてみたものだ。後の「恋の力学」シリーズなどはここらへんから始まっていた、といっても良いだろう。そしてこの頃の[Scraps]系の話題としては、がある。少し前に、この「さなえちゃん」を描いた漫画の作者からメールを頂いたのがとても私には印象深かった。そして、1999年の上半期から選んでみると、まずは
というところだろう。ハードディスクの情報を可視化することで情報圧縮・エントロピーを考えてみた一話である。そして、同じような「可視化シリーズ」の一つである- 感温液晶でNotePCの発熱分布を可視化する- 熱いところで感じてみたい St.Valentine 記念 - (1999.02.14)
- NotePCの発熱分布を比べてみたい- お熱いのがお好き SOME LIKE IT HOT - (1999.02.15)
そして、1999年の下半期はもう自分で言うのも何だが傑作揃いである。大体、書いているペースが自分でも驚くくらいのハイペースだ。月当たりの話の数を数えてみると、
- 7月 9話
- 8月 9話
- 9月 8話
- 10月 8話
- 11月 11話
- 12月 9話
この頃の「お薦めの話」はいっぱいある。例えば、
に始まった「文章可視化シリーズ」や、で始まった「ASCIIアートシリーズ」だろう。から始まる「江戸五色不動シリーズ」は江戸にロケまで行ったので、とても思い出深い話の一つである。しかも、妙な偶然のせいでまるで小説の中に迷い込んだような気持ちになったものだ。そして、WEBページを作る上では
などもどうしても外せない。そして、この後結構続くことになるという「恋の力学」シリーズもこの時期に始まっている。そして、この頃の一番人気が何と言ってもだろう。この「ミニスカート」系の話の流れは以降も続くことになるのが自分では意外でもあり、残念でもある。それはさておき、ナンセンス系ではなんてのも面白い話だと思う。そして、1999年の終わりはやはりこれが「お気に入り」の話である。また、[Scraps]系の話がこの時期にはやたらいっぱいあるのが面白いところだ。その内からいくつかピックアップするとこんな感じだろうか?- [Scraps]絵馬 - どこにもいないよ- (1999.07.09)
- 新宿駅は電気羊の夢を見るか- 意識とは何か - (1999.07.10)
- [Scraps]合掌 - キレイはキタナイ、キタナイはキレイ- (1999.08.01)
- [Scraps]いつかきっと -掌の中の答え - (99.11.03)
- 「文学論」と光学系 - 漱石の面白さ-(2000.02.27)
- 恋の力学 恋の相関分析編- 「明暗」の登場人物達の行方 - (2000.04.01)
- 恋の力学 恋のグラフ配置編- 「明暗」の収束を見てみよう - (2000.04.02)
- 恋する心を見てみたい - 恋のきっかけはどの出来事?- (2000.05.14)
- 恋の形を見た人は - 恋の相対性理論- (2000.05.17)
さて、今回は2000年上半期までの話の中から「私の好きな話」を振り返ってみた。とはいえ、私の好きな話=他の人の好きな話ではないようだし、他の話も適当に眺めて頂いたら良いかなぁ(私が)、と思うのだった。
2000-09-07[n年前へ]
■草枕で遊ぶ 
それが人間の科学なんだよ、と誰かが言った
どうしても割り切らないではいられない話だと知った時、それが人間の科学なんだよ、と...(半神)
私が大好きな演劇の一つに「半神」がある。レイ・ブラッドベリ・萩尾望都・野田秀樹の共作とも言うべきこの「半神」の中で1/2+ 1/2 = 2/4 という「螺旋方程式」の謎に対して
「その謎はひとごと(他人事)ではない。」というレトリックが使われていた。ここでは「ひとごと」という言葉の意味を巧みに切り替えて、「論理をすり替え」ている。こんなレトリックが私は気持ち良くて大好きだ。急斜面のコブを巧みにすり抜けていくスキーのモーグル選手みたいで、爽快な感じがするのである。
「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」
ところで野田秀樹ほど言葉遊びが巧みな人もそうそういないだろうが、この
「ひとごと(人ごと)でないのだから、その謎は化け物に関わることだ。」というもののオリジナルはもちろん夏目漱石の草枕の冒頭部だろう。その草枕の冒頭部分を部分的に抜粋するとこんな感じになる。
智に働けば角が立つ。情に棹させば流される。意地を通せば窮屈だ。とかくに人の世は住みにくい。人の世を作ったものは神でもなければ鬼でもない。やはり向う三軒両隣りにちらちらするただの人である。ただの人が作った人の世が住みにくいからとて、越す国はあるまい。あれば人でなしの国へ行くばかりだ。人でなしの国は人の世よりもなお住みにくかろう。
この
「人の世が住みにくい」という巧みな論理はどうだろうか?私には実に爽快な自然な飛躍に感じられる。目的とする場所へ、巧みに言葉を切り替えていくことで自然に辿り着くこんなやり方がとても気持ちが良い、と私は思う。
->「人が作った世が住みにくいならば、人でないものの世なら住みやすいだろうか」
-> 「人でなしの国へ行くばかり」
-> 「人でなしの国は人の世よりもなお住みにくい」
ところで、以前
でも挙げたとても面白いの中でもこの草枕冒頭部の論理のすり替えについて触れられていて、その中で漱石の「文学評論」中の「漱石とあたたかな科学」小山慶太著 講談社学術文庫
花は科学じゃない、しかし植物学は科学である。鳥は科学じゃない、しかし動物学は科学である。文学はもとより科学じゃない、しかし文学の批評または歴史は科学である。というレトリックに対しても
「文学のどこに観察、実験、数理解析が施せるのであろうか。」と書かれている。もちろん、「文学を味わうのは心であるべき」ということは言うまでもない。しかし、「文学のどこに観察、実験、数理解析が施せるのであろうか。」というところで思考を停止してしまうのは、実に残念であると私は思う。そこで、今回は「草枕」を題材に採って、いつものように単語解析をすることで、適当な考察をしてみることにした。「草枕」に対して数理解析をして遊んでみたい、と思うのである。
「草枕」は青年画家がブラブラしたり、ボうっと色々なことを考えたりする話だ。そして、いかに芸術が生まれるかということに考えてみたりするのである。例えば、冒頭では
住みにくさが高じると、安い所へ引き越したくなる。どこへ越しても住みにくいと悟った時、詩が生れて、画が出来る。という具合である。また、途中の部分では
して見ると四角な世界から常識と名のつく、一角を磨滅して、三角のうちに住むのを芸術家と呼んでもよかろう。というように書かれている。
一体、青年画家がどんな時に「画」を書くのかどうかを知るために、他の単語の出現分布と「画」の出現分布を調べてみることにした。今回、ノミネートしてみた単語は「角」・「男」・「女」である。
角が立つ四角い人の世の中で三角のうちに住むのが芸術家であるならば、その「角」と「画」の相関は調べてみたいと思うハズである。また、これまでに様々な「男」と「女」の関係を考えてきた「できるかな?」であるから、やはりここは「男」と「女」もノミネートしないわけにはいかないだろう。
そこで、「画」・「角」・「男」・「女」の各語の出現分布を調べてみたのが次の各図である。もちろん、今回も前回
と同じく、wordfreqを使って解析を行った。 | 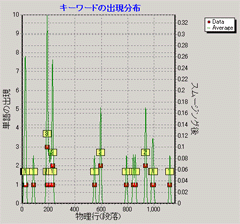 |
 |  |
次に、「画」の出現分布に対するそれぞれの言葉の出現分布の相関値を計算してみよう(なお、計算の安定のために、適当な平滑化をここでは行っている。)主人公の青年画家がどんな時に「画」について考えたり、描こうとしたりするかを考えてみるわけである。その計算結果が次の表である。
角 | 男 | 女 | |
相関係数 | 0.08 | 0.09 | 0.21 |
そして、さらにこれをグラフにしてみたものが、下のグラフである。
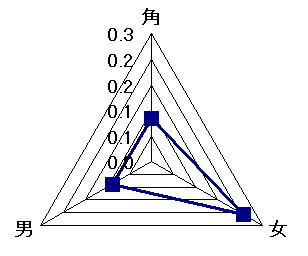 |
おやおや、困ったなぁ。ちょっと、この「画」と「女」の相関の高さはちょっと異常だなぁ。「角」や「男」の出現分布の「画」に対する相関は0.1以下であるが、何と「女」は0.2を越えている。最初は、「画」と「角」を強引に結びつけて話を終わらせるつもりでいたのになぁ。これじゃぁ、主人公はヒロインを前にするときだけ芸術家になるみたいじゃないの。おかしいなぁ、こんな狙いじゃなかったのになぁ...まるで、「草枕」は漱石の前田卓へのラブレターみたいに思えてきてしまうではありませんか...
う〜ん、これはどっか間違えたかなぁ。まぁ、いいや。今日はもう眠いし。
ところで、「草枕」ではどのようにして文学・音楽・絵画などのさまざまな芸術が生まれて来るかが書かれている。そして、冒頭の「半神」でも、シャム双生児の姉妹とともに「螺旋方程式」の謎を追いかけるうちに、人の心を動かす孤独と音が生まれてくるようすが語られていく。
 |
今回の相関解析では、「芸術は女を前にしたときに生まれる」というフザケタ結果に終わってしまったが、その真偽についてはまたいつか考えてみることにして、とりあえず今回は草枕の中の台詞で話を強引に終わらせたいと思う。
越す事のならぬ世が住みにくければ、住みにくい所をどれほどか、寛容て、束の間の命を、束の間でも住みよくせねばならぬ。ここに詩人という天職が出来て、ここに画家という使命が降る。あらゆる芸術の士は人の世を長閑にし、人の心を豊かにするが故に尊とい。
2000-09-17[n年前へ]
■円周率は約3で良いか 
「円周率を約3にするのなら、授業の名前も約算数とか約数学にすべきである。言葉の厳密な意味にかかずらう文化系としてはっきりとそう訴えておく。」from 朝日新聞の朝刊「eメール時評」いとうせいこう。この意見は、「そんなこと、最初からそうだ」ってことが判っていない「典型的な勘違い」だと思う。シミュレーションや計測をすると、そういうことが理解できていない人達に限って、盲目的に信じてしまう傾向があるが、それとどこか似ている。文化系とか理科系とかそんなこと関係なくて、単にいとうせいこうが「何かを絶対視したがってる」だけ。ゲーデルの爪の垢を煎じて飲んでみるのも良いのではないだろうか?だけど、いとうせいこうの「ノーライフキング」は古田足日の「盗まれた町」を受け継ぐ児童文学の名作だと思う。いや、古田足日の「盗まれた町」があまりにも早すぎた作品だったと言うべきか。