2002-02-20[n年前へ]
■「やおい」の評価演算子 
ベクトルの彼方で待ってて II
 東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
東京駅近くの飲み屋「美少年」で、日本酒利き酒セットを目の前にしながら、私は珍しく「日本の政治」について話していた。といっても、単にそれは話し相手が社会部に属する新聞記者だったからである。で、その時の話題は小泉首相と福田官房長官の話だったろうか?
「福田X小泉っていうのは、結構上手くやっているのかな?」と私が言うと、おもむろに
「あれは、福田X小泉じゃなくて、絶対あれは小泉X福田なのー」とその記者が言ったのである。何を言っているのかその意味がよく判らないまま、「ん〜?」と私が首を傾げていると、繰り返し
「福田X小泉と小泉X福田は全然意味が違うのー」と言い始めるのである。何が何だか訳がわからない。じゃぁ、何か?小泉X福田だと小泉純一郎が総理大臣で福田康夫が官房長官だけど、福田X小泉だと福田康夫が総理大臣で小泉純一郎が官房長官になるとでも言うのか??政治の世界では、言う順番で総理大臣が決まるとでも言うのか?と私が口をはさむと、
「そう。ただ、ちょっと政治の世界とは違う世界かも〜。政界じゃなくて、やおい界ではー。」と言うのだ。なんだコイツ?政界は判るけど、やおい界って一体何処の世界の話だ??と、困惑する私も構わず、そこから延々と長い演説が始まった…。その大河ドラマのようにやたらと長い話を要約すると、
- やおい → 一部の女性が好む「男性同士の恋愛もののストーリー」のこと
- X → やおいの世界で恋愛の関係を示す記号。例えば、AさんとBさんが恋に落ちるであれば、Aさん×Bさんと表す。で、ここで重要なのは先に位置する方が「攻め役」となって、後に位置する方が「受け役」となる…。つまり、例えばサド侯爵とレオパルド・マゾッホであれば攻め役がサド侯爵で、受け役がマゾッホなので、サド×マゾなのである。決して、マゾ×サドではない…
で、日本酒を飲みながら、まだまだ続くその話に悪酔いしていると、「カップルの順序が重要なんだー」という言葉を聞いて、ふと中学の頃の数学の授業を思い出した。その頃、大学を出てまだ一年目の斉藤慶子似の数学の先生と話していたときに、「Hくん、あのね掛け合わせる順序が違うと結果も違っちゃう計算もあるのよ」と教わったことがあった。そんな言葉から私は未知の「数学の世界」をかいま見たりしたのである。 今考えてみれば、新任の斉藤慶子似の女性教師の個人授業なのだから、行列・ベクトルの掛け算の順序なんかじゃなくて、「もっと違う順序」を手取り足取り教えてくれても良かったんじゃないか、とか思ったりするし、そうすれば、私は未だ見ぬ「大人の世界」を覗き見ることができたのではないか、と思ったりもするのだけれど、そんなことは残念ながら無くて、私はただ「行列・ベクトルの世界」を覗いただけだったのである。
で、そんな昔話を思い出したせいか、頭の中でこんな風に思ったのである。そういえば、これまで「できるかな?」では数多く「恋の力学」でも遊んできた。ただ、そこでは「惹かれ合う恋心の大きさ」だけに注目して、そのカップルの中での役割などは考えたことがなかった。そこで、今回は「やおい」のカップルの「役割・順序」に注目し、その「役割・順序」を評価する演算子を行列・ベクトルの掛け算になぞらえながら考えてみることで、これまでと同じく色々な「恋の形」を眺めてみたいと思う。
まずは、色々な人物(実際の人物であったり、小説などの登場人物であったり)のタイプを二次元空間に配置しよう。「この人は結構攻め役が合いそう」とか「この人は絶対受け役が合うのだー」という適性を
- 攻めベクトル
- 受けベクトル
 |
そして、カップリング適性では「A×B、B×Aが全然違う」ということから、外積(ベクトル積)をそのまま流用して、適当な評価関数を作ってみるのが自然だろう。まず、
カップリング適性ベクトル = (攻め度(s)、受け度(m))と表記して、例えばAさんのカップリング適性ベクトルを(As, Am)と表すことにしてみよう。すると、Aさんが「攻め」でBさんが「受け」のカップリング適性は、この二人の適性ベクトルのベクトル積として表すことができる。つまり、
A×Bのカップリング適性 = ( As * Bm - Am * Bs )となるわけである。式を眺めれば判るように、Aさんの攻め度が高くて、Bさんの受け度が高ければ、この評価関数は高い値を返す。つまり、「A×Bの順序は正しいのだー」という評価を返す。つまり、「A×B」はなかなか良いカップルだー、と教えてくれる。また、もしAさんの受け度が高くて、Bさんの攻め度が高ければ、低い値を返す。つまり、「A×Bの順序は絶対間違ってるのだー」と評価してくれるのである。なんともありがたいことに(いや別にありがたくはないか…)、この「やおいのカップリング評価演算子」が「福田X小泉」と「小泉X福田」のどちらが自然なのかを教えてくれるのだ。試しに、上のサドくんとMくんであれば、「サドくん×Mくん」= (100,0)×(0,100) = 100*100 - 0*0 = 10000でとっても「良い感じ」でああるが、「Mくん×サドくん」= (0,100)×(100,0) = 0*0 - 100*100 = -10000で「このカップリングは絶対順序が違うー」と判るわけである。
= Aさんの攻め度 * Bさんの受け度
- Aさんの受け度 * Bさんの攻め度
とりあえず、今回はこの評価演算子を作成するところまでで終えたいと思うが、いずれこの「やおいの評価演算子」を武器にして、いつか(?)「やおいの世界= やおい界」に限らず、色んな数多くの恋の関係を目に見えるようにしてみたいと思う。そして、これまで数多く考えてきた「恋の〜シリーズ」を充実させていきたいと思うのである。
ところで、今回のカップリング適性評価演算子は基本的に外積そのものである。つまり、この演算が返す値は「二人のベクトルでできる平行四辺形の面積」に等しい。つまりは、「二人のベクトルでどれだけ色んな違うことがきでるか」を示す尺度である。そして、その値は二人のベクトルが直交する時、すなわち二人のベクトルが重ならず独立である時に最大値となる。つまりは、「二人のベクトルが違えば違うほど大きく」なる。例えば、先の「サドくん×Mくん」であれば二人のS,M趣向が完全に正反対であったからとてもお似合いのカップルになったのである。
これをいわゆる恋の話で考えてみると、とっても独立な二人、趣味が重ならない二人がお似合いだということになる。なるほど、そんなカップルも世の中にはたくさんいることだろう。そんな人達を「外積タイプのカップル」と呼ぶことができると思う。
一方、趣味が重ならないカップルだけでなくて、世の中にはそれとは正反対の「趣味が重なる良いカップル」も数多くいる。それは「内積タイプのカップル」である。内積はA,Bベクトル間の正射影に比例する量であって、つまりは「二人の重なるベクトルの大きさ」である。それは例えば、相手の中に自分を重ね合わせるような「二人の重なる部分が二人を結びつけるようなカップル」なのである。
「理系と文系」・「男と女」が対極的なものでも、相反するものでもないのと同じく、「外積カップルと内積カップル」も別に二つに分けられるようなものではないだろう。「外積タイプの恋」も「内積タイプの恋」が混じり合って、それぞれに良いところもあれば、危ういところもあって、などと想像してみるのも面白いに違いない。そして、さらにはもしかしたらベクトル空間で萌えることができるようになったりするかもしれない。
そういえば、ふと考えてみると以前「恋の形を見た人は」で最後に引用した本橋馨子の「兼次おじ様シリーズ」は男性同士の恋の話だった。つまりは「やおい」の話だった。そこで、もう一度そのセリフを最後に飾って眺めてみようと思うのである。
「愛はどんな形をしているか知っているか?」「見た事ないからわかりません。」「そうだ、誰も見た者はないのに、誰もが当然のように形づけて受け入れている...
もし愛に優劣を決めるものがあればなんだろう?... 異性愛か、同性愛か、そんなものじゃない …たとえ、どんな形だろうと選ぶのはおまえ自身だよ。」
2002-03-16[n年前へ]
■何と、女性は宇宙であった。 
今の宇宙は「熟女」なのだ
私の職場には「オレは女性は絶対年上が良いと思うね」と断言する人達がいる。その一方で「自分より年下でなければ人じゃないスよ」という、「それは人間として如何なモノか」と問いたくなるような新入社員一派もいる。
ある日、何かの打ち上げでビールを飲みながら、そんな「熟女vsロリ」大論争を聞いている時、私はふと思ったのである。あれ?女性の「色っぽさ」ってどんな色なのだろう?色っぽさって、そういえば何色なんだろう?ちょっと眺めてみたい気がするな〜。
それに…、その女性の「色っぽさの色」は年を重ねると、どんな風に変化していくのだろう?「色っぽさ」はどんなカーブで成長していくのだろう?と、そんな風に思った私は、今回「女性の色っぽさ」が何色であるか、そしてそれは女性が年を重ねるにしたがってどう変化していくかを調べて、眺めてみることにした。
これまでも、「できるかな?」ではさまざまな抽象的なもののイメージ(=画像)をネットワーク上から多数集めそれらの色分布を調べることで、それらの抽象的なもののイメージ(=印象)を目に見える形にしてきた。だから、ある程度は「色っぽい」というのがどんな色だかは想像がつく。例えば、下は「心の色はどんな色?」で調べた「笑顔・童話・心・エロ」の色である。
 |
こんな風に、ネットワーク上から多数の画像を集めれば、抽象的なものであっても「目に見える色」にすることができる。ましてや、女性の色っぽさなどは、もちろんもとより「色っぽい」というくらいだから、「目に見える色」にするのは簡単なことだ。いつもと違うのは、女性が年を重ねるにしたがって「色っぽさ」がどう変化していくかを調べるので、ちょっと定量的に扱ってやらなければならないだけである。
そこでまずは、HiraxNetMosaicMakerに多数の画像の「色の平均値」を出力するウィンドーを付けたてみた。
 |
そして、いつもと同じように「GuruguruImage+Iria+HiraxNetMosaicMaker」トリオでさまざまな女性の画像を収集し、その「色っぽさ」を調査することにしてみた。ネットワーク上からいつものようにゴッソリ集めた画像は全部で6種類である。まずは、年齢に応じた女性の呼び名である
- 幼女
- 少女
- 熟女
- 老女
また、上の四つのような年齢だけではなくて、さらに「何らかの属性が付加されている」
- 女子大生
- 淑女
さて、早速調査した結果を眺めてみることにしよう。下の表が色んな女性の「色」と「色っぽさ」を示した結果である。ちなみに、ここで「色っぽさ」というのはa*a+b*bを示している。つまり、どれだけ「色っぽい」かを示す数値である。
| L | a* | b* | 色っぽさ | |
| 幼女 | 79.5 | 1.4 | 1.5 | 4.21 |
| 少女 | 76.0 | 2.3 | 3.9 | 20.5 |
| 熟女 | 76.7 | 3.8 | 4.6 | 35.6 |
| 老女 | 74.3 | 2.9 | 3.9 | 23.6 |
| 女子大生 | 76.9 | 1.6 | 3.4 | 14.1 |
| 淑女 | 79.3 | 2.3 | 3.2 | 15.5 |
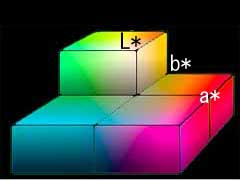
そして、この数値を見ながら、下のLab色空間とそこに配置した「笑顔・童話・心・エロ」のイメージを眺めてみよう。すると、例えば熟女の「色」がa*=3.8,b*=4.6と群を抜いて高く、「心」度も高いが「エロ」度も高い、となるのである。そして、その結果「色っぽさ」は他の倍以上の値を示しているのだ。そう、熟女が一番色っぽいのである。先の「オレは女性は絶対年上が良いと思うね」という一派が大喜びしそうな結果が出てしまったが、別に私は彼らからワイロをもらっているわけでないのである。
 |  |
次に、これらの女性の「色っぽさ」をそれぞれ相当する年齢位置に配置して、女性の「色っぽさ」の年齢カーブを示してみたものが下のグラフである。
すると、生まれてそれほど時間が経っていない幼女は実に「色っぽくない」が、年を経て少女を過ぎる頃にはやがて色づいてくることがよく判る。そして、熟女となる頃には、まさに「熟した女」としか言いようがないくらい、その「色っぽさ」は最高潮に達するのである。そして、さらに年を重ねると、「色っぽさ」は薄まるが、それでも少女よりはまだまだ色っぽい、という事実が目に見える形で私たちの前に姿を現すのだ。
 |
また、このグラフの女性の「色っぽさ」のカーブを試しに二次関数で近似してみると、
「色っぽさ」=-0.015 x (年齢)^2 + 1.4 x (年齢) + 2.3となる。試しにこれをhiraxの「色っぽさ」成長近似関数(暫定版)と呼ぶことにしよう。この式さえ知っておけば、再び飲み屋で「熟女vsロリ」大論争が勃発した折りには、この式を片手に、「きみいくつ?えっ、にじゅうごー!?自分より年下でなければ人じゃない?それは違うよ。少なくとも君が45歳くらいまではね。」と冷静にアドバイスしたりすることができるわけだ。
ところで、このグラフ中の「女子大生」と「淑女」を眺めてみると、平均的な女性の「色っぽさカーブ」から大きく外れて「色っぽくない」ことが判ると思う。そう、学問に打ち込む女性も淑女も「色っぽい度」は低いのである。当たり前である。エラーチェッカーとして入れた「女子大生」と「淑女」の調査結果からも、今回の調査方法も世間のあり方も間違っていないことが見てとれるのである。
また、今回多数採集した「幼女・少女・熟女・老女」をそれぞれ平均化してみた「色」を下に示してみた。これが各女性達の「色っぽさ」=「色」の変化チャートなのだが、あなたはこの中のどの色に「色っぽさ」を感じるだろうか?
 |
さて、こんな「女性の色っぽさ変化チャート」を眺めていると、先日発表された「あの研究報告」を連想してしまう人も多いに違いない。そう、先日米ジョンズ・ホプキンズ大学の2人の天文学者が約20万個の銀河の光を全て平均化した結果、すなわち「宇宙の色はこんな色」と発表したあれである。「多数の何かを集めて平均化して、そのものの色を目に見える形にする」という方法論も、そしてそれがちょっとした遊び心でやるというところも、今回の話とよく似た(だけど大違いの)あの研究報告である。
あの研究報告の「宇宙の色」と今回の「女性の色っぽさ」ではそれを求める方法もよく似ているが、驚くべきことに何とその結果もうり二つなのである。ちなみに、下が彼らが報告したIIIE gammaを用いて変換した場合の「宇宙の色」の変化チャートである。ビッグバンから今日、そして遙か未来までの宇宙の色の変化を示したものだ。
 |
そう、先に示した女性達の「色っぽさ」=「色」の変化チャートと瓜二つなのである。女性の色の変化は「宇宙の色」の変化そのものなのだ。「元始、女性は実に太陽であった」と平塚らいてうは「青鞜」の創刊の辞に書いたが、それは素晴らしく正しかったのである。そして、女性は太陽どころではなくて、何と、女性は宇宙であったのだ。そして、今日の宇宙は(私の勝手な偏見から言えば)ちょうど熟女の「色っぽさ」なのである。今の宇宙はまさに「熟れ頃」なのである。こんな私の研究成果をもしも平塚らいてうに知らせることができたら、一体彼女は何と言うだろうか?う〜ん、平塚らいてうが何というかは判らないが、ルパン三世の峰不二子であれば、きっとこう言うに違いない。
…男ってバカね。
2002-04-24[n年前へ]
■視線のベクトルは未来に向くの? 
マンガのストーリーの方向を顔向きで探る 前編
一年くらい前から、コンビニで300円ほどの安いコミックをたまに買うようになった。休日の早朝、コンビニで発泡酒とおつまみを買って、ついでにそんな安いコミックを買って、そして、ビールを飲みながらそれを読むのがワタシの休日のささやかな(だけど至高の)幸せなのである。そんな至高の幸せをかみしめるとある休日、286円の西岸良平の「三丁目の夕日」を読みながら、ワタシはふと思ったのである。
これまで、「できるかな?」では、様々な小説、例えば「星の王子さま」「明暗」「こころ」「草枕」「失楽園殺人事件」といった小説を色々と解析してきた。そして、その中の主人公達がどんな風に動いていくのかとか、作者が何を考えているかとか、あるいは、犯人は誰かであるのか、などを調べてきた。何でそんなことを考えるの、と人には聞かれそうだけれども、とにもかくにもワタシはそんなことを考えてきたのである。そして、さらにふと考えてみれば、ワタシの至高の幸せを支える素晴らしき286円のマンガ本に関して、ワタシはストーリー構造などを真剣に考えてみたり、調べてみたりしたことはなかったのである。イケナイ、イケナイ、こんなことでは「恩知らず」野郎としてワタシにはバチが当たってしまうに違いないのである。
そこで、今回「コミックの中のストーリー構造」について調べてみたい、と思う。コミックの中で主人公達がどのような方向へ進もうとしているのか、あるいはその歩みの中で主人公達は一体何を考えているのか、などについて少し調べてみることにしたのである。
これまで、小説中のストーリー構造や主人公達の動く方向を調べるときには、「特定の言葉や主人公達」が登場する位置を調べたり、あるいは他の言葉や登場人物との相関を調べたりしてきた。それでは、一体マンガのストーリー構造や主人公達の動く方向を調べるにはどうしたら良いだろうか?そんなものどうやって調べるの?と一瞬悩んでしまいそうではあるが、ちょっと考えてみればそれはとても簡単なのである。小説と違って、マンガでは登場人物達がちゃんと見えるカタチで描かれているのである。主人公達がどの方向を向いているかがちゃんと描かれているのである。そしてまた、主人公やその周りの人々や、ありとあらゆる人々がどんな方向を向いているかがもうありのままにちゃんと描かれているのである。
だったら話は実に簡単、マンガの中の登場人物達の向きを刻々調べてみれば、そのマンガのストーリーの中で主人公達がどちらへ向かって何を見ながら動いているかが判る、というわけだ。実に即物的でシンプルなアプローチである。
善は急げ、というわけで、早速今さっきまで読んでいた手元に掴んだままの西岸良平の「三丁目の夕日 ジングルベル」の中から、「霜ばしら」という短編を題材にして、その中の主人公の顔の向きを調べてみることにした。ある恋人同士の、とても楽しくて、そしてとても悲しい物語である。
まずは、マンガのコマ中の登場人物達の向きと角度の対応表を下の表のように定めた。登場人物がコマ中で右方向を向いているときに0度とし、正面方向(すわなち読者方向)を向いている時が90度。コマの左方向を向いていれば180度である。そして、280度では真後ろを向いているという具合である。
270 | ||
180 | 0 | |
90 |
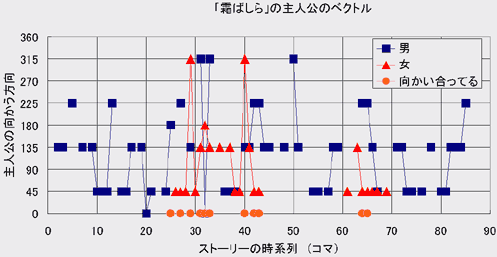
このようにコマの中に登場する主人公達の向きを数値化することにして、話の冒頭から結末までの各コマ中での主人公(周平)とその恋人(アキちゃん)の向きを調べてみたのが下のグラフである。青色の四角が主人公で、赤色の三角がヒロインである。また、その二人が向かい合ってる場合には朱色の丸を方向=0の位置に書き入れてみた。グラフ中では水平軸がストーリーの時系列で、左端が話の冒頭であり、右端が話の結末、そして縦軸が「主人公達の向かう方向」である。また、ヒロインのアキちゃんが途中の2カ所にしか現れないのは少しばかり悲しいストーリーのせいだ。この「霜ばしら」は主人公とアキちゃんの涙を誘う悲しい物語なのである。
左端 = 話の冒頭 右端 = 話の結末 縦軸 = 主人公達の向かう方向
|
このグラフを少し眺めていると大体の特徴が見えてくるだろう。すなわち、
- 主人公達はほとんど45、135、235度の3方向しか向いていない
- それ以外の向き(例えば315度)を向く場合などは、ほとんどが「向き合っている」場合である
- そして、135度の方向を向いていることが圧倒的に多い。
しかし考えてみれば、これらの特徴はごく当たり前なのである。まずは、舞台やテレビと同じく、登場人物達は読者にお尻を向けるわけにはそうそういかない。読者に顔を見せずにお尻を向けていたら、誰が誰だかよく判らなくなってしまうに違いない。だから、登場人物達はあまり後ろを向くわけにはいかない。どうしても、主人公達は文字通り「前向き」にならざるをえない。もし、後ろを向くとしたら、それは文字通り登場人物達に「後ろを向かせる」何らかの強い意図に基づく場合以外ありえないに違いない。それが、例えば他の誰かと「向き合って」いる場合であったり、あるいは他の表現意図に基づくものであろう。
また、日本におけるマンガが右から左に読まれていくのであるから、読者の視線の動きの中では「右のコマ= 過去」「左のコマ = 未来」と時間感覚が成立している。マンガを読む私たちの視線のベクトルは右から左、過去から未来へと進んでいるのである。すなわち、「マンガの中の話の流れ= マンガの中の時間・因果の流れ」をスムーズにするためには、主人公達が過去なり未来なりのコマの方向を向くことで、時間の流れ=因果の流れをスムーズに受け継ぐのが自然だと考えられる。過去に発生した「何か」に応えた反応をするならば、主人公達は当然右を向くし、そうでないならば通常は時間の流れる先の向き= 左側を向くことになるだろう。
すると、マンガの中の登場人物達は読者に対して「前向き」であって、なおかつ時間の流れる方向に前向きの「左側」を向くのがごく自然である、ということになって、「コマの中の主人公達は135度の方向を向くことが圧倒的に多い」ということになるのだろう。まぁ、当たり前の話である。
そしてさらには、こんな風にも考えられる。「右<->左」方向は時間の流れに対する主人公達の向きであって、「前向き<->後ろ向き」は登場人物達が文字通り「前向きであるか」あるいは、あるいは「後ろ向きであるか」という「主人公達の内たる気持ちの向き」ではないだろうか、とも考えられるのである。
だから、例えばこの「霜ばしら」の結末の部分80コマ以降を見ると、45->135->225度という主人公のベクトルの変化がある。これは主人公が「過去に向かう向き(死んでしまったヒロインへを見る向き)→未来に向かう方向へ進む→未来に向かう(だけど、やはり亡くなってしまったヒロインをたまに振り返りながら)」というまさに主人公のベクトルを描き出しているのではないだろうか、と思うのである。そんな風に眺めてみれば、最後のコマの主人公の向きが「何かを振り返りながら、だけど未来へと歩いていく様子」をまさに映し出しているようにも見えるのである。ストーリーはここに書くわけにはいかないけれど、こんな想像も割と良い線をいってるのかもしれない、と思ってみたりするのだ。
 |
こんな風に、単にマンガの登場人物の向きだけで主人公達の向かうベクトルを探る、なんていうことが乱暴なのはさらさら承知の上である。こんな人物の配置解析によるストーリー解析が的を射ているのか、あるいは的を外しまくっているのかは、ぜひこのマンガを読んで実際に判断してみてもらいたい、と思うのである。
さて、こんな風に舞台の右と左、上手と下手に対してどんな風に登場人物達が向かっていくのか、なんてことを考えるといろんな想像が広がってとても面白いのである。時間の進むベクトルであるLeftStage(舞台から見ると逆なんてことは言わずに)に消えていく登場人物達(例えば今回の話では恋人アキちゃんを亡くしてしまった主人公)は「残されたもの達」を連想させてみたり、あるいは、色んなものを眺める私たちの視線のベクトルは本当に未来に向いているのかな?などと色んな想像や空想を駆けめぐらせてみることも、それはそれでとても趣深いことだなぁと思うのである。
2002-04-27[n年前へ]
■視線のベクトルは未来に向くの? from 麗美さん 
偶然ですが、4月24日に、NHKで夜中に「BSマンガ夜話」の再放送をやっていて、その中で韓国のマンガ「アイランド」を取り上げて、この「できるかな?」と同じような分析を夏目房之介がやっていました。もちろん夏目氏の場合は「できるかな?」のような理系的・数量的な分析ではなく、ストーリーに則った文学的・文芸的分析だったわけですが、両者とも同じような結論ですね。ということで、人物の配置解析によるストーリー解析は的を射ていると思います。
夏目氏の分析でおもしろかったのは、韓国ではマンガの台詞は当然ハングルだから縦書きではなく横書きになります。そのため、日本のマンガのように右から左に読み進むのではなく、左から右に読む進む。つまり、韓国では左開きなのです。とすると、絵も基本的に左右が逆転されます。右に向いた顔は未来指向・肯定的・明るさを表わし、左に向いた顔は過去回顧・否定的・暗さを表わします。じゃあ、日本のマンガの絵をそのまま左右反転させればいいかといえばそうでもないらしいです。台詞が横書きであることも関係して、視線の動きが単純に左右反転では合致しないわけです。
日本人の未来は左で、韓国人の未来は右なんですね(笑い)
(リンク)
2002-06-03[n年前へ]
■カードサイズの「画像探偵セット」!? 
お手軽線数メーターを作るのだ
「どんなものでも、自分の目で眺めてみた〜い」と、ワタシはいつでも思う。世の中スベテのものを、自分の目で眺めてみた〜いと思う。しょんべん小僧が空中に描き出す放物線、巨乳ギャルにロックオンするオッパイ星人の目の動き、ビデオにかかるモザイクの向こう、はたまた田代まさしが恋い焦がれるミニスカートの結界の秘密、とにかく世の中のものスベテを何でもかんでも眺めてみたい、覗いてみたい、とワタシはいつも思っているのである。(とはいえ、誤解されると困るので念のために書いておくが、もちろんミニスカートの中を覗いたりはしないのだ)
そんなわけで、ワタシのケータイのストラップには「ちっちゃなちっちゃな虫メガネ」がついている。この虫メガネを武器にして、ワタシは色んなモノを覗くのがクセになっている。スーツ姿で出張している時だって、おもむろにこの虫眼鏡を取り出して、色んなものを覗いてみたりしているのである。
 |
だから、毎朝届けられる新聞に折り込まれているチラシやカタログを眺めるときだって、そんなカタログに「ちっちゃなちっちゃな虫メガネ」を向けてみて、その「虫メガネ」を通して、カタログがどんな風に印刷されているかをよく眺めてみる。下の左のようなカラーの綺麗なカタログだって、「虫メガネ」を通して眺めてみると、右の拡大写真みたいに、四色(シアン、マゼンダ、イエロー、ブラック)が規則正しく並んでいるようすが見えてくるのである。離れてみればキレイな写真が「虫メガネ」を通して眺めてみるだけで、こんな風に様子が変わるなんてとても不思議な気分になったりするのである。まるで、女性の化粧のように不思議で、こんな四色の手品はとても面白いのである。
| (左上と右上部分はマゼンダとシアンだけを見やすくしてみた)
|
で、こんなカタログの拡大図を眺めていると、四色に分けられた色がどんな風に並べられ形作られているかを、知りたくてたまらなくなったりする。つまり、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とか思うわけである。もちろん、この画像に二次元フーリエ変換などをかけさえすれば(周波数解析をすれば)、「どんな角度で・どんな間隔で色が並べられているか」ということは知ることができるけれど、まさかワタシの頭の中でそんな作業ができるわけはない。かといって、このカタログを読み込むための「画像読みとり装置」や「解析をするためのコンピューター」を毎日持ち歩くなんてこともできるわけもない。
そこで、「どんな間隔でこの色は配置されているのだろう?」とか「一体、どんな角度でこの色は並べられているのだろう?」とかいう疑問の答えがすぐ判るように、先日こんなカード、ぴったりクレジットカードサイズの透明シートに規則的なパターンを印刷したカード、を作ってみた。名付けて、Peco-Chartなのである。
これはもちろん、判る人には判るだろうが、ハンディ「線数メーター」というモノである。一言で言えば、画像の周波数解析をとっても簡単にすることができる手品の小道具のようなカードなのだ。
 |
例えば、さっきのカタログの上にこのPeco-Chartを重ねて置いてみると、アラ不思議、何やらヘンな模様、不思議なモアレ模様が浮かび上がってくる。下の左の写真、あるいは右の拡大写真を眺めてみればマゼンダとシアンの同心円がハッキリと浮かび上がっているのが見えるだろう。例えば、シアン色の場合は75°の角度で175線(175線/inch)位の位置、そしてマゼンダ色の場合は45°の角度で同じく175線位の位置を中心として、同心円状のモアレ模様が浮かび上がっている。
つまり、「このカタログはシアンは75°の角度方向に1インチ辺り175個のドットが並べられていて、マゼンダのドットは45°の角度方向に並べられている」、ということを、このPeco-Chartを重ねて置いてみさえすればたちどころに知ることができるのである。
 |  |
 |
こんなペラペラのカードで周波数解析ができるなんてとても不思議に思えたりもするけれど、ちょっと考えてみればこれはごく当たり前の話である。
でも似たようなことをしたように、モアレというものは「二種類以上の何らかの模様(パターン)が干渉して発生する」ものである。つまり、ある意味「二つのパターンの相関をとる」ということである。そしてまた、少し考えてみれば「画像の周波数解析」というものは「対象となる画像」と「基準関数(三角関数etc.)」の間で相関を調べることと同じである。だから、「基準となるパターン」を「対象となる画像」の上に重ねてみた時に見えるモアレのパターンは「対象となる画像」の周波数解析結果を実は示していると考えてみても良いのである。だから、このPeco-Chartはクレジットカードサイズのペラペラなちっぽけなヤツではあるのだけれど、実は色んな画像の周波数解析をしてくれるスゴイヤツだったのである。そして、こんなポケットに入るほど小さい線数メーターははなかなか無いので、、カード入れからコイツを華麗に取り出してみせたりすると、うらやましがる人もとても多く(仕事柄、画像出力に関わる人達が多いから)、なかなかに気持ちが良いのである。 とはいえ、自慢してばかりでは何なので、さらに大量に配布すべく新たなPeco-Chart二号機をデザインしてみた。それが、下の名付けてPecochartproである。
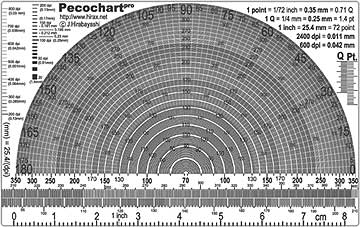 |
このPecochartproの謳い文句はその名の通り「プロ仕様」というわけで、画像出力に関わっている何人ものベータテスター達(自分も含めて)の感想をもとにして、
- 70線から350線までの線数とスクリーン角度の測定ができる「線数・角度メーター」(分解能を2線単位から1線単位へと二倍向上、スクリーン角度のガイドは2.5度刻み)
- 90線から410線までの線数を高精度(0.25線刻み)に計測することができる「線数メーター」(新機能)
- 線・文字の太さを計測できる「線幅スケール」(新機能)
- 〜30級、〜30ポイントまでの文字サイズ(級数、ポイント)測定ができる「文字スケール」(Peco-Chartと同じ)
- 「8cm定規」(Peco-Chartと同じものを使い勝手はそのままにコンパクト化)
- そして、便利な「画像に関する換算表」(内容を従来比75%増量)
それにしても、何か自分に役に立つツールを作るというのは本当に楽しい作業だった。手作りツールぎゃらりい脇色彩研究所ではないけれど、こんな「hirax.netオリジナルグッズ」をいっぱい作って「探偵セット」ならぬ「できるかな?セット」として、面白メールをくれた方にプレゼントとかしてみたら楽しいんだろうなぁ、と思うのである。というわけで、そんなツールをせっせと作るのだぁ、なんてことを実は計画中なのでした、ハイ。